指数を正の整数だけでなく、\(0\),負の整数,有理数,実数に拡張していきます。
・正の整数の指数
\(n\)を正の整数とするとき、\(a\)(実数)を\(n\)回掛け合わせたものを \(a^n\) で表し、\(a\)の\(n\)乗とよびます。
また、\(a,a^2,a^3・・・,a^n\) をまとめて\(a\)の累乗(るいじょう)とよびます。そして、\(a\)の累乗\(a^n\)に対して右上の数\(n\)を、この累乗の指数とよびます。
一般に正の整数\(m,n\)について次の指数法則が成り立ちます。
①\(a^ma^n=a^{m+n}\)
②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\)
これらが成り立つことは具体例を考えると分かりやすいです。
①は
\(a^5a^3\)
\(=(a・a・a・a・a)(a・a・a)\) (\(a\)が(5+3=8)個掛けられている)
\(=a^{5+3}\)
となるので、\(a^5a^3=a^{5×3}\) にはならないことが分かります。
②は
\((a^5)^3\)
\(=(a^5)(a^5)(a^5)\)
\(=(a・a・a・a・a)(a・a・a・a・a)(a・a・a・a・a)\) (\(a\)が(5×3=15)個掛けられている)
\(=a^{5×3}\)
③は
\((ab)^3\)
\(=(ab)(ab)(ab)\)
\(=(a・a・a)(b・b・b)\)
\(=a^3b^3\)
そして一般の\(m,n\)についても同じことがいえるので、上記指数法則①~③が成り立つことになります。
・\(a^0\)、負の整数の指数
指数が\(0\)や負の整数の場合、\(a\)の累乗をどのように定義するのがよいでしょうか。
指数が正の整数のときの\(a\)の累乗を並べて図示してみると次のようになります。
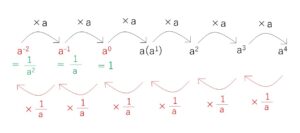
右側にいくにつれて、\(a\)倍され、指数の数が\(1\)増えているのでこれを逆にみると、
左側にいくにつれて、\(\displaystyle\frac{1}{a}\)倍されて、指数の数が\(1\)減っています。
(\(\displaystyle\frac{1}{a}\)倍を考えているので、\(a≠0\)としておきます)
そうすると、\(a^0=a×\displaystyle\frac{1}{a}=1\)
と定義するのがよさそうです。
そしてこのように \(a^0=1\) (\(a≠0\))と定義することで上記指数法則①~③
①\(a^ma^n=a^{m+n}\)
②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\)
は、\(m,n\)が\(0\)のときも成り立つことがわかります。
例えば \(m=0\) のとき①は
\(a^0a^n=1・a^n=a^{0+n}\)
となりますね。
\(3・2^2\), \(3・2^1\),\(3・2^0\)を考えると順に、3に2を2回掛ける、3に2を1回掛ける、3に2を0回掛ける(なにもしない)、となるので、\(2^0=1\) となることがわかります。
「2を0回掛ける=0を掛ける」とはなりません。
ただどうしても納得できない人は、定義なのでそう決めると割り切ってもよいです。
(1)\(a^0=1\) と同じように \(0^0=1\)
(2)\(0^4,0^3,0^2,0^1\) (全部\(0\)) の列を考えると、\(0^0=0\)
の両方の捉え方があるからです。
続いて指数が負の整数での場合ですが、\(a^0\)のときと同様に考えると
\(a^{-1}=a^0×\displaystyle\frac{1}{a}=\displaystyle\frac{1}{a}\)
\(a^{-2}=a^{-1}×\displaystyle\frac{1}{a}=\displaystyle\frac{1}{a^2}\)
\(a^{-3}=a^{-2}×\displaystyle\frac{1}{a}=\displaystyle\frac{1}{a^3}\)
と定義すればよさそうです。
一般には、\(n\)を正の整数とするとき、
\(a^{-n}=\displaystyle\frac{1}{a^n}\)
となります。ただし分母に\(0\)とならないように、\(a≠0\) としておきます。
そして指数が負の整数のときも指数法則①~③が成り立ちます。
例えば \(m=3\), \(n=-4\) で①は
\(a^3a^{-4}\)
\(=a^3・\displaystyle\frac{1}{a^4}\)
\(=\displaystyle\frac{1}{a}\)
\(=a^{-1}\)
\(=a^{3-4}\)
※一般の\(m,n\)でも、\(m,n\)が整数なので、\(a\)が掛けられている(割られている)数がカウントできるので指数法則①~③が成り立ちます。
さらに指数法則①~③を用いることで割り算や、分数の累乗について次のような計算が行えます。
\(m,n\)が整数、\(a,b≠0\) のとき
①’
\(a^m÷a^n\)
\(=\displaystyle\frac{a^m}{a^n}\)
\(=a^ma^{-n}\)
\(=a^{m-n}\)
③’
\((\displaystyle\frac{a}{b})^m\)
\(=(ab^{-1})^m\)
\(=a^mb^{-m}\)
\(=\displaystyle\frac{a^m}{b^m}\)
以上のことをまとめると次のようになります。
\(a≠0\), \(n\)が正の整数のとき
\(a^0=1\), \(a^{-n}=\displaystyle\frac{1}{a^n}\)
\(a≠0\), \(b≠0\) で、\(m,n\) が整数のとき
①\(a^ma^n=a^{m+n}\) ①’ \(a^m÷a^n=a^{m-n}\)
②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\) ③’ \((\displaystyle\frac{a}{b})^m=\displaystyle\frac{a^m}{b^m}\)
ただし今後の指数が有理数や無理数のときは、\(a>0\) という前提がつきます。
長くなりそうなので、指数が有理数(分数)、無理数のときについては次回に回したいと思います。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→累乗根、有理数・無理数の指数