前回に引き続いて、有理数や無理数の指数について学んでいきます。
・累乗根
有理数(分数)の指数を考える準備として、累乗根について整理しておきます。
\(a\)を実数とするとき、正の整数\(n\)に対して\(n\)乗すると\(a\)となる数、すなわち
\(x^n=a\)
となる数\(x\)を\(a\)の\(n\)乗根といいます。
\(n=3\), \(a=8\) とすれば \(x^3=8\) の解は実数範囲では\(x=2\) のみなので(因数分解すれば残りは虚数)
「\(8\)の3乗根(3乗すると\(8\)になる数)は実数では\(2\)」
\(n=4\), \(a=16\) とすれば \(x^4=16\) の解は実数範囲では \(x=±2\) なので
「\(16\)の4乗根(4乗すると\(16\)になる数)は実数では\(±2\)」
となります。これらの例のようにキレイな数で表されない場合については平方根の\(√\)のように記号(根号)をつかって表します。(以下参照してください)
また、2乗根,3乗根,4乗根・・・をまとめて累乗根といいます。\(x^n=a\) の解(累乗根)は複素数範囲では、\(n\)個存在することになりますが、このうち実数のみをとりあげて考えていきます。
実数解がいくつあるかは、\(y=x^n\) のグラフの形状を考えると分かりやすいです。
(複素数平面(数Ⅲ)で考えてもできます)
\(x^n=a\) の実数解は、\(y=x^n\) の形状が\(n\)の偶奇によって異なるので場合分けします。
①\(n\)が奇数のとき
\(y=f(x)=x^n\) とすると
\(f(-x)=(-x)^n=(-1)^nx^n=-x^n\)
より奇関数(原点対称)となる。\(x≧0\) のときだけ考えると単調増加(\(x\)が増えると\(f(x)\)も増加)するのでグラフは次の通り。
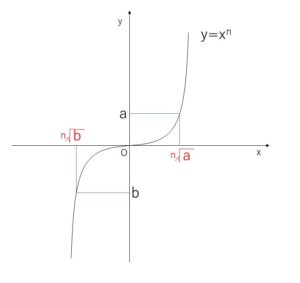
図より、\(x^n=a\) を満たす\(x\)、つまり\(a\)の\(n\)乗根は\(a\)の正負0に関係なくただ1つ存在して、それを \(\sqrt[n]{a}\) と表します。
また、グラフから\(a>0\) のときは、\(\sqrt[n]{a}>0\)、\(a<0\)のときは \(\sqrt[n]{a}<0\) です。
特に\(a=0\)のときは、 \(\sqrt[n]{0}=0\) です。
②\(n\)が偶数のとき
\(y=f(x)=x^n\) とすると
\(f(-x)=(-x)^n=(-1)^nx^n=x^n\)
より偶関数(\(y\)軸対称)となる。\(x≧0\) のときだけ考えると単調増加(\(x\)が増えると\(f(x)\)も増加)するのでグラフは次の通り。
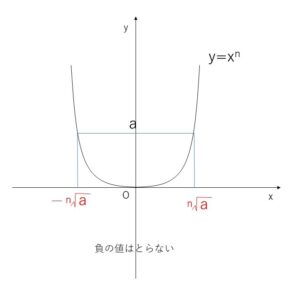
図より、\(x^n=a\) を満たす\(x\)、つまり\(a\)の\(n\)乗根は
\(a>0\)のとき2つ存在して、そのうち正の方を \(\sqrt[n]{a}\) 、負の方を\(-\sqrt[n]{a}\) と表します。
\(a=0\)のときは1つだけ存在して、それは\(\sqrt[n]{0}=0\) です。
\(a<0\)のときは、偶数乗して負になる実数は存在しないため、\(a\)の\(n\)乗根は存在しないことになります。(グラフからも明らか)
\(a\)の\(n\)乗根(実数)と、\(\sqrt[n]{a}\) は違うものです。
例えば、\(16\)の4乗根は\(±2\)の2つを表しますが、\(\sqrt[4]{16}\)は\(16\)の4乗根の正のほうなので\(2\)のみを表します。
平方根のときも似たような話がありますね。
以下\(n\)を偶奇関係無しでまとめるために、\(a>0\) として、\(\sqrt[n]{a}\)のほうのみを扱うことにすると次のことが言えます。
\(a>0\) のとき、\(\sqrt[n]{a}\) は次の条件を満たすただ1つの数となる。
\((\sqrt[n]{a})^n=a\) (\(n\)乗すると\(a\)になる)
\(\sqrt[n]{a}>0\)
そしてこのことから累乗根について次の性質が成り立ちます。
\(a>0\), \(b>0\) かつ \(m,n,p\)が正の整数のとき
①\(\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}\) (同じ\(n\)乗根はまとめられる)
②\(\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\displaystyle\frac{a}{b}}\) (同じ\(n\)乗根はまとめられる)
③\((\sqrt[n]{a})^m=\sqrt[n]{a^m}\)
④\(\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\)
⑤\(\sqrt[n]{a^m}=\sqrt[np]{a^{mp}}\) (\(p\)乗したら\(p\)乗根とって帳尻あわせ)
①のみ証明します。(②~⑤も同じように証明できます)
左辺の\(n\)乗を考えると
\((\sqrt[n]{a}\sqrt[n]{b})^n\)
\(=(\sqrt[n]{a})^n(\sqrt[n]{b})^n\)
\(=ab>0\)
ここで、\(\sqrt[n]{a}>0\), \(\sqrt[n]{b}>0\) より
\(\sqrt[n]{a}\sqrt[n]{b}>0\) だから
\(\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}\)
・有理数の指数
いよいよ有理数(分数)の指数について考えていきます。
ここでは \(a^{\frac{m}{n}}\) がどのような数になるかを指数法則が成り立つことから逆算して定めていきたいと思います。
\(a>0\)として 指数法則
①\(a^ma^n=a^{m+n}\)
②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\)
において、②で\(m=\displaystyle\frac{3}{4}\), \(n=4\) のとき成り立つとすると
\((a^{\frac{3}{4}})^4=a^{\frac{3}{4}\cdot4}=a^{3}\)
となるので、\(a^{\frac{3}{4}}\)は、\(a^3\)の正の4乗根と定義します。
つまり
\(a^{\frac{3}{4}}=\sqrt[4]{a^3}\)
となります。
また負の有理数については、①で\(m=-\displaystyle\frac{1}{3}\), \(n=\displaystyle\frac{1}{3}\) のとき成り立つとすると
\(a^{-\frac{1}{3}}a^{\frac{1}{3}}\)
\(=a^{-\frac{1}{3}+\frac{1}{3}}\)
\(=a^0\)
\(=1\)
よって
\(a^{-\frac{1}{3}}=\displaystyle\frac{1}{a^{\frac{1}{3}}}\)
このような考え方に従って、一般に次のように指数が有理数の累乗を定めます。
\(a>0\), \(m,n\)が正の整数、\(r\)が正の有理数のとき
(1)\(a^{\frac{m}{n}}=\sqrt[n]{a^m}\)
とくに \(a^{\frac{1}{n}}=\sqrt[n]{a}\)
(2)\(a^{-r}=\displaystyle\frac{1}{a^r}\)
そしてこのように指数が有理数である累乗を定めると、累乗根の性質①~⑤を用いることで、指数が整数のときと同じように指数法則が成り立つことが分かります。
\(a>0\), \(b>0\) で、\(r,s\)が有理数のとき
①\(a^ra^s=a^{r+s}\) ①’ \(a^r÷a^s=a^{r-s}\)
②\((a^r)^s=a^{rs}\)
③\((ab)^r=a^rb^r\) ③’ \((\displaystyle\frac{a}{b})^r=\displaystyle\frac{a^r}{b^r}\)
①のみ示すと (②~⑤も証明できます)
\(r,s\)は有理数なので、\(m,n,m’,n’\) (\(n,n’≠0\)) を整数とすれば
\(r=\displaystyle\frac{m}{n}\), \(s=\displaystyle\frac{m’}{n’}\) とおけて
\(m,n\)が整数であることに注意すると
\(a^ra^s\)
\(=a^{\frac{m}{n}}×a^{\frac{m’}{n’}}\)
\(=\sqrt[n]{a^m}×\sqrt[n’]{a^{m’}}\)
\(=\sqrt[nn’]{a^{mn’}}×\sqrt[nn’]{a^{m’n}}\)
\(=\sqrt[nn’]{a^{mn’}\cdot a^{m’n}}\)
\(=\sqrt[nn’]{a^{mn’+m’n}}\)
\(=a^{\frac{mn’+m’n}{nn’}}\)
\(=a^{\frac{m}{n}+\frac{m’}{n’}}\)
\(=a^{r+s}\)
・無理数の指数
最後に指数が無理数の場合の累乗について考えていきます。
どう定義するかというと、その無理数に近い(極めて近い)有理数を考えるのです。
例えば、無理数 \(π=3.141・・・\) について、\(2^{π}\) の値は
指数が、\(3\), \(3.1\), \(3.14\), \(3.141\) (全て有理数) のときを順に考えると
\(2^3=8\)
\(2^{3.1}=8.57・・・\)
\(2^{3.14}=8.81・・・\)
\(2^{3.145}=8.821・・・\)
となり、桁数をいくらでも増やすことである一定の値に近づきます。この一定値の値を\(2^{π}\) と定義するわけです。(厳密には、上に有界な単調増加数列は一定値に収束するということになります)
このようにして任意の実数\(x\)について、\(a^x\)を定めます。(ここでも\(a>0\)としておきます)
またざっくりとした説明になりますが、有理数の値によって近づけて定義しているので、指数が実数のときにも指数法則が成り立つことになります。
※ちなみに無理数についても指数を定義したのは、指数関数のグラフを考えるときに有理数のみだと、とびとびのグラフ(途切れたグラフ)になってしまうからです。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→指数の計算① back→0や負の整数の指数