今回からは絶対値を含む、1次方程式・不等式について学びます。
・絶対値を含む方程式・不等式の解き方
原則的には、絶対値の中身に文字が含まれるときは中身の正負で場合分けをしていきます。しかし、以下の特殊な場合は場合分けせずに一気に解くことができます。(場合分けしても解くことができます)
\(c>0\)のとき
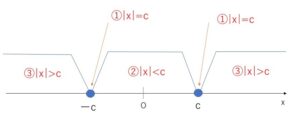
① \(|x|=c\) の解は、 \(x=±c\)
② \(|x|<c\) の解は、 \(-c<x<c\)
③ \(|x|>c\) の解は、 \(x<-c,x>c\)
① \(|x|=c\) の解は、 \(x=±c\)
② \(|x|<c\) の解は、 \(-c<x<c\)
③ \(|x|>c\) の解は、 \(x<-c,x>c\)
数直線を考えれば明らかです。
ちなみに\(c=0\)のとき解は、①の場合は\(x=0\)の1つで、②は解なし、③は0以外のすべての実数となります。\(c<0\)のときは①②は解なしで、③はすべての実数となります。(絶対値≧0からわかります)
(例題)
(1) \(|x-3|=6\)
(2) \(|x+1|≦3\)
(1) \(|x-3|=6\)
(2) \(|x+1|≦3\)
(解答)
(1)
\(x-3=±6\)
よって、\(x=-3,9\)
(1)
\(x-3=±6\)
よって、\(x=-3,9\)
(2)
\(-3≦x+1≦3\)
\(-3≦x+1≦3\)
よって \(-4≦x≦2\)
※両方とも場合分けしても解くことができます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。