これから関数の微分を利用した、最大・最小値に関して学んでいきますが、最初に少しだけ知識の整理をしておきます。
・区間
\(3≦x≦5\), \(-4<x<-1\) , \(x>6\) などの不等式を満たす実数\(x\)の集合を区間とよびます。
また、イコールつきの不等式
\(a≦x≦b\)
で表された区間を閉区間
イコールなしの不等式
\(a<x<b\)
で表された区間を開区間
といいます。
なお閉区間は、\([a,b]\) 開区間は \((a,b)\) と表されることもあります。
関数の閉区間における最大最小値を求めるには、「極値・端点」が候補となるのでこれらを調べて比べることになります。一方開区間では端点は候補になりません。
(例題)次の関数のそれぞれの区間における最大値・最小値を求めよ。
(1) \(y=-2x^3+15x^2-36x\) (\(1≦x≦3\))
(2) \(y=3x^4-4x^3-12x^2+3\) (\(-1≦x≦1\))
(解答)
(1)
\(y=-2x^3+15x^2-36x\) (\(1≦x≦3\)) において
\(y’=-6(x-2)(x-3)\)
増減表とグラフは次の通り
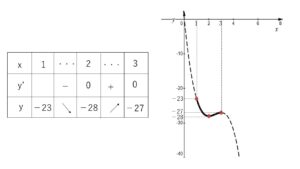
したがって
最大値 \(-23\) (\(x=1\))
最小値 \(-28\) (\(x=2\))
(2)
\(y=3x^4-4x^3-12x^2+3\) (\(-1≦x≦1\)) において
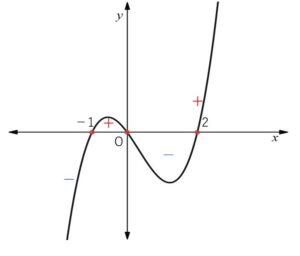
\(y’=12x(x+1)(x-2)\)
これらの値の近くを考えてもよいですし、\(y’\)のグラフと\(x\)軸との交点の\(x\)座標が、\(-1,0,2\) であることと、3次関数のグラフの形状(交点が3つなので極値をもつ形状になる)から考えてもよいです。
増減表とグラフは次の通り。
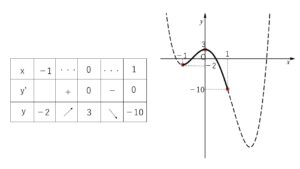
したがって、
最大値 \(3\) (\(x=0\))
最小値 \(-10\) (\(x=1\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→最大・最小値①(文字含む) back→極値をとるxの存在範囲