今回は、グラフの対称移動について見ていきます。→(2-1)グラフの平行移動 では具体的な2次関数についてまず考えましたが、今回は一般的な曲線の対称移動について最初に考えていきます。
曲線 \(y=f(x)\)を対称移動するとどのような方程式に変化するでしょうか。
・一般的な曲線の対称移動
曲線 \(y=f(x)\)上の点を\((X,Y)\)とすると、\(Y=f(X)\)・・・①
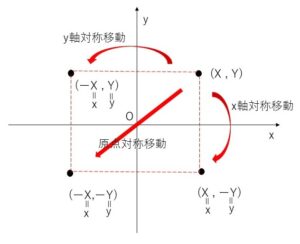
\(x\)軸,\(y\)軸,原点について対称な点を\((x,y)\)とします。求めたいものは\(x,y\)の関係式です。\(x\)と\(X\)、\(y\)と\(Y\)の関係式はそれぞれ以下のようになります。
(\(x\)軸について対称) \(x=X\) \(y=-Y\)
(\(y\)軸について対称) \(x=-X\) \(y=Y\)
(原点について対称) \(x=-X\) \(y=-Y\)
それぞれを①に代入して、
(\(x\)軸について対称) \(-y=f(x)\)
(\(y\)軸について対称) \(y=f(-x)\)
(原点について対称) \(-y=f(-x)\)
つまり
(\(x\)軸について対称) \(y\) → \(-y\)
(\(y\)軸について対称) \(x\) → \(-x\)
(原点について対称) \(x\) → \(-x\) \(y\) → \(-y\)
とおきかえればよいことになります。
よって具体的な2次関数 \(y=ax^2+bx+c\) については以下のようになります。
(\(x\)軸について対称) \(-y=ax^2+bx+c\)
(\(y\)軸について対称) \(y=a(-x)^2+b(-x)+c\)
(原点について対称) \(-y=a(-x)^2+b(-x)+c\)
(\(y\)軸について対称) \(y=a(-x)^2+b(-x)+c\)
(原点について対称) \(-y=a(-x)^2+b(-x)+c\)
これは覚えるのではなく、一般的な曲線の場合の考え方で \(x,y\)の符号がどう入れ替わるのかを理解することが大切です。
(例題)
放物線 \(y=x^2-2x+5\) を次のものに関して対称移動した放物線の方程式を求めよ。
(1) \(x\)軸 (2) \(y\)軸 (3)原点
放物線 \(y=x^2-2x+5\) を次のものに関して対称移動した放物線の方程式を求めよ。
(1) \(x\)軸 (2) \(y\)軸 (3)原点
(解答)
(1)
\(y\)を\(-y\)におきかえて、\(-y=x^2-2x+5\)
よって \(y=-x^2+2x-5\)
\(y\)を\(-y\)におきかえて、\(-y=x^2-2x+5\)
よって \(y=-x^2+2x-5\)
(2)
\(x\)を\(-x\)におきかえて、\(y=(-x)^2-2(-x)+5\)
よって \(y=x^2+2x+5\)
\(x\)を\(-x\)におきかえて、\(y=(-x)^2-2(-x)+5\)
よって \(y=x^2+2x+5\)
(3)
\(x\)を\(-x\)に \(y\)を\(-y\)におきかえて
\(-y=(-x)^2-2(-x)+5\)
よって \(y=-x^2-2x-5\)
\(x\)を\(-x\)に \(y\)を\(-y\)におきかえて
\(-y=(-x)^2-2(-x)+5\)
よって \(y=-x^2-2x-5\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
ここまで読んで頂きありがとうございました。