高次方程式の実数解の存在範囲に関する問題について見ていきます。
(例題1)
3次方程式 \(2x^3-3x^2-12x+a=0\) の解が、2つの異なる負の数と1つの正の数であるための\(a\)の条件を求めよ。
\(a=-2x^3+3x^2+12x\) (\(=f(x)\)) とすると
直線 \(y=a\) と 曲線 \(y=f(x)\) の共有点が3つであり、それら共有点の\(x\)座標が2つ負の数で、1つ正の数である場合を考えればよい。
\(f'(x)=-6(x+1)(x-2)\) より増減表とグラフは次の通り。
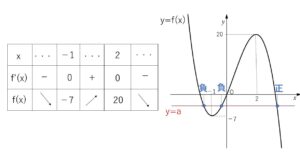
このうち2つが負、1つが正のときは交点の\(x\)座標を考えると、\(-7<a<0\) です。
ちなみに、
\(a=0\) だと 「負,0,正」
\(0<a<20\) だと 「負,正,正」
となります。
したがって条件を満たす\(a\)の値の範囲は
\(-7<a<0\)
(例題2)
4次方程式 \(3x^4-4x^3-12x^2-k=0\) が互いに異なる4つの実数解をもつための\(k\)の値の範囲は \(□<k<□\) である。このとき、4つの実数解のうち最大のものを\(α\)とする。\(k\)が上の範囲を変化するとき、\(α\)のとり得る値の範囲は \(□<α<□\) である。
(解答)
(前半部分)
\(3x^4-4x^3-12x^2=k\) において \(f(x)=\)(左辺) とすると、
\(y=f(x)\) と \(y=k\) の共有点が4つ存在するときの\(k\)の値の範囲を求めればよい。
\(f'(x)=12x(x+1)(x-2)\) より
\(f'(x)=0\) となるのは、\(x=-1,0,2\) で増減表とグラフは次の通り。
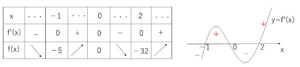
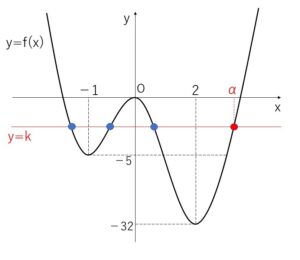
したがって、方程式が異なる4つの実数解をもつときは
\(-5<k<0\)
(後半部分)
したがって、\(f(x)=-5\) と \(f(x)=0\) を解けばよいのですが、それぞれ重解が \(x=-1\), \(x=0\) となることに着目するとスムーズに解くことができます。
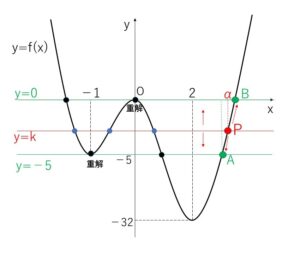
4つの交点のうち\(x\)座標が最大となるものを点\(P\)とすると、点\(P\)は図の点\(A,B\)の間を動く。よって、
\((点Aのx座標)<α<(点Bのx座標)\)
点\(A\)について
\(3x^4-4x^3-12x^2=-5\) を解くと
\(3x^4-4x^3-12x^2+5=0\)
\((x+1)^2(3x^2-10x+5)=0\)
\(3x^2-10x+5=0\) より
\(x=\displaystyle\frac{5±\sqrt{10}}{3}\)
このうち 点\(A\)の\(x\)座標は大きい方だから
\(x=\displaystyle\frac{5+\sqrt{10}}{3}\)
点\(B\)についても同様に
\(3x^4-4x^3-12x^2=0\) を解くと
\(x^2(3x^2-4x-12)=0\)
\(3x^2-4x-12=0\) より
\(x=\displaystyle\frac{2±2\sqrt{10}}{3}\)
このうち大きい方が点\(B\)の\(x\)座標となるので
\(x=\displaystyle\frac{2+2\sqrt{10}}{3}\)
以上から
\(\displaystyle\frac{5+\sqrt{10}}{3}<α<\displaystyle\frac{2+2\sqrt{10}}{3}\)
(参考)
残りの3つの解の範囲も同様に求めることができます。
実数解を小さい順に、\(β,γ,δ\) とすると図より
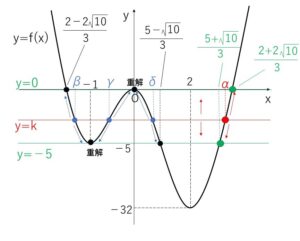
\(\displaystyle\frac{2-2\sqrt{10}}{3}<β<-1\)
\(-1<γ<0\)
\(0<δ<\displaystyle\frac{5-\sqrt{10}}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→微分法と軌跡・領域① back→不等式と微分②