曲線と接線で囲む図形の面積や面積比のまとめです。
・2次関数(2つの接線と囲む面積)
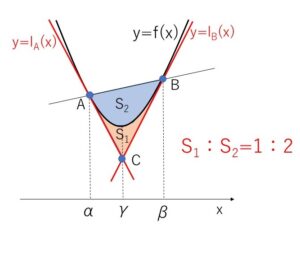
放物線 \(y=f(x)=ax^2+bx+c\) (\(a≠0\)) 上の2点\(A,B\) (点\(A\)の\(x\)座標のほうが小さい) における接線と \(y=f(x)\) とで囲まれる図形の面積を\(S_1\)、直線\(AB\)と\(y=f(x)\)とで囲まれる図形の面積を\(S_2\)とする。\(A,B\)の\(x\)座標をそれぞれ\(α,β\) (\(α<β\)) とすると
\(S_1=\displaystyle\frac{|a|}{12}(β-α)^3\)
\(S_2=\displaystyle\frac{|a|}{6}(β-α)^3\)
\(S_1:S_2=1:2\)
(証明)
<流れは、「2接線を求める→2接線の交点\(C\)の\(x\)座標\(γ\)を求める→積分する」です>
\(f'(x)=2ax+b\)
点\(A\)における接線 \(y=l_A(x)\) は
\(y=(2aα+b)(x-α)+aα^2+bα+c\)
整理して
\(y=2aαx-aα^2+c\)・・・①
点\(B\)における接線 \(y=l_B(x)\) は
\(y=(2aβ+b)(x-β)+aβ^2+bβ+c\)
整理して
\(y=2aβx-aβ^2+c\)・・・②
①-②より
\(2a(α-β)x-a(α^2-β^2)=0\)
\(2a(α-β)x=a(α+β)(α-β)\)
よって2接線の交点の\(x\)座標\(γ\)は
\(x=γ=\displaystyle\frac{α+β}{2}\)
したがって
\(S_1=\displaystyle\int_α^γ|f(x)-l_A(x)|dx+\displaystyle\int_γ^β|f(x)-l_B(x)|dx\)
\(=\displaystyle\int_α^γ|a(x-α)^2|dx+\displaystyle\int_γ^β|a(x-β)^2|dx\) (接するので2乗の形になる)
\(=|a|\displaystyle\int_α^γ(x-α)^2dx+|a|\displaystyle\int_γ^β(x-β)^2dx\)
\(=|a|\left[\displaystyle\frac{(x-α)^3}{3}\right]_α^γ+|a|\left[\displaystyle\frac{(x-β)^3}{3}\right]_γ^β\)
\(=|a|\displaystyle\frac{(β-α)^3}{24}-|a|\displaystyle\frac{(α-β)^3}{24}\)
\(=|a|\displaystyle\frac{(β-α)^3}{24}+|a|\displaystyle\frac{(β-α)^3}{24}\)
\(=\displaystyle\frac{|a|}{12}(β-α)^3\)
また、直線\(AB\)の方程式を \(y=l_{AB}(x)\) とおくと
\(S_2=\displaystyle\int_α^β|l_{AB}(x)-f(x)|dx\)
\(=\displaystyle\int_α^β|-a(x-α)(x-β)|dx\)
\(=|-a|\displaystyle\int_α^β|(x-α)(x-β)|dx\) (\(α≦x≦β\) で絶対の中身は\(0\)以下)
\(=|a|\displaystyle\int_α^β-(x-α)(x-β)dx\)
\(=\displaystyle\frac{|a|}{6}(β-α)^3\)
以上より
\(S_1:S_2=\displaystyle\frac{1}{12}:\displaystyle\frac{1}{6}\)
\(=1:2\)
・2次関数(2つの2次関数と共通接線)
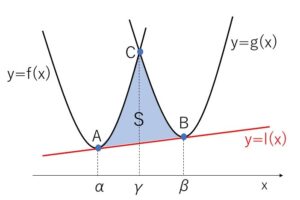
2次の係数が同じである 放物線 \(y=f(x)=ax^2+bx+c\) と \(y=g(x)=ax^2+b’x+c’\) (\(b≠b’\)) の共通接線を \(y=l(x)\) とする。接点を\(x\)座標の小さいほうから点\(A,B\)とし、それぞれの\(x\)座標を\(α,β\) (\(α<β\)) とする。2つの放物線と接線で囲まれる面積\(S\)は、
\(S=\displaystyle\frac{|a|}{12}(β-α)^3\)
(証明)
<流れは「2つの放物線の交点\(C\)の\(x\)座標\(γ\)を求める→積分する」です。>
2つの放物線の交点を\(C\)とし、その\(x\)座標を\(γ\)とする。
\(ax^2+bx+c=ax^2+b’x+c’\) より
\((b-b’)x=c’-c\)
\(x=γ=\displaystyle\frac{c’-c}{b-b’}\)・・・①
\(A\)における接線は、\(y’=2ax+b\) より
\(y=(2aα+b)(x-α)+aα^2+bα+c\)
整理して
\(y=(2aα+b)x-aα^2+c\)・・・②
\(B\)における接線は、\(y’=2ax+b’\) より
\(y=(2aβ+b’)(x-β)+aβ^2+b’β+c’\)
整理して
\(y=(2aβ+b’)x-aβ^2+c’\)・・・③
②③が一致するから
\(2aα+b=2aβ+b’\)・・・④
\(-aα^2+c=-aβ^2+c’\)・・・⑤
④より
\(b-b’=2a(β-α)\)
⑤より
\(c’-c=a(β^2-α^2)\)
これらを①に代入して
\(γ\)\(=\displaystyle\frac{a(β^2-α^2)}{2a(β-α)}\)\(=\displaystyle\frac{α+β}{2}\)
したがって面積\(S\)は
\(S=\displaystyle\int_α^γ|f(x)-l(x)|dx+\displaystyle\int_γ^β|g(x)-l(x)|dx\)
\(=\displaystyle\int_α^γ|a(x-α)^2|dx+\displaystyle\int_γ^β|a(x-β)^2|dx\)
\(=|a|\displaystyle\int_α^γ(x-α)^2dx+|a|\displaystyle\int_γ^β(x-β)^2dx\)
\(=|a|\left[\displaystyle\frac{(x-α)^3}{3}\right]_α^γ+|a|\left[\displaystyle\frac{(x-β)^3}{3}\right]_γ^β\)
\(=|a|\displaystyle\frac{(β-α)^3}{24}-|a|\displaystyle\frac{(α-β)^3}{24}\)
\(=|a|\displaystyle\frac{(β-α)^3}{24}+|a|\displaystyle\frac{(β-α)^3}{24}\)
\(=\displaystyle\frac{|a|}{12}(β-α)^3\)
・3次関数
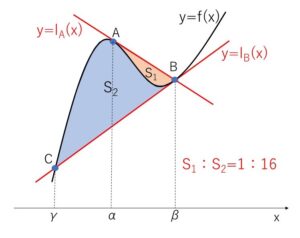
3次関数 \(y=f(x)=ax^3+bx^2+cx+d\) 上の点\(A\)における接線 \(y=l_A(x)\) と \(y=f(x)\) の交点を\(B\)、点\(B\)における接線 \(y=l_B(x)\) と \(y=f(x)\) の交点を\(C\) とする。点\(A,B,C\)が互いに異なるとき、\(y=l_A(x)\) と \(y=f(x)\) で囲まれる図形の面積を\(S_1\), \(y=l_B(x)\) と \(y=f(x)\) で囲まれる図形の面積を\(S_2\)とし、点\(A,B\)の\(x\)座標をそれぞれ\(α,β\) とすると
\(S_1=\displaystyle\frac{|a|}{12}(β-α)^4\)
\(S_2=\displaystyle\frac{|a|}{12}\cdot16(β-α)^4\)
\(S_1:S_2=1:16\)
(証明)
<流れは「接点\(C\)の\(x\)座標\(γ\)を求める→積分する」です>
\(f'(x)=3ax^2+2bx+c\) より
点\(A\)における接線の方程式は
\(y=(3aα^2+2bα+c)(x-α)+aα^3+bα^2+cα+d\)
整理して
\(y=(3aα^2+2bα+c)x-2aα^3-bα^2+d\)
\(y=f(x)\) と連立して
\(ax^3+bx^2+cx+d=(3aα^2+2bα+c)x-2aα^3-bα^2+d\)
整理して
\(ax^3+bx^2-(3aα^2+2bα)x+2aα^3+bα^2=0\)
(\(x=α\) が重解になることに着目して)
\(a(x-α)^2(x+2α+\displaystyle\frac{b}{a})=0\)
よって点\(B\)の\(x\)座標\(β\)は、\(α\)を用いて
\(β=-(2α+\displaystyle\frac{b}{a})\)・・・①
と表せる。
同様に考えると点\(C\)の\(x\)座標は\(γ\)は、①で \(α→β\) にすればよいので
\(γ=-(2β+\displaystyle\frac{b}{a})\)・・・②
面積\(S_1\)は
\(S_1=\left|\displaystyle\int_{α}^{β}\{l_A(x)-f(x)\}dx\right|\)
\(=\left|\displaystyle\int_{α}^{β}-a(x-α)^2(x-β)dx\right|\)
\(=|a|\left|\displaystyle\int_{α}^{β}-(x-α)^2\{(x-α)+α-β\}dx\right|\)
\(=|a|\left|-\displaystyle\int_{α}^{β}(x-α)^3dx+(β-α)\displaystyle\int_{α}^{β}(x-α)^2dx\right|\)
\(=|a|\left|-\left[\displaystyle\frac{(x-α)^4}{4}\right]_α^β+(β-α)\left[\displaystyle\frac{(x-α)^3}{3}\right]_α^β\right|\)
\(=|a|\left|\displaystyle\frac{(β-α)^4}{12}\right|\)
\(=\displaystyle\frac{|a|}{12}(β-α)^4\)
面積\(S_2\)については、上端と下端を入れ替えても、被積分関数の差を入れ替えても符号が変わるだけなので、\(S_1\)において 「\(α→β\), \(β→γ\) 」とすればよく
\(S_2=\displaystyle\frac{|a|}{12}(γ-β)^4\)
ここで①②より
\(γ-β=2(α-β)\) だから
\(S_2=\displaystyle\frac{|a|}{12}\cdot2^4(α-β)^4\)
\(=\displaystyle\frac{|a|}{12}\cdot16(β-α)^4\)
したがって
\(S_1:S_2=1:16\)
・4次関数(二重接線)
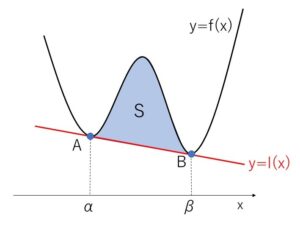
4次関数 \(y=f(x)=ax^4+bx^3+cx^2+dx+e\) と異なる2点\(A,B\)で接する接線を \(y=l(x)\)とする。\(y=f(x)\) と 接線 \(y=l(x)\) で囲まれる図形の面積\(S\)は、\(A,B\)の\(x\)座標を\(α,β\) (\(α<β\)) とすると
\(S=\displaystyle\frac{|a|}{30}(β-α)^5\)
面積\(S\)は
\(S=\displaystyle\int_{α}^{β}|f(x)-l(x)|dx\)
\(=\displaystyle\int_{α}^{β}|a(x-α)^2(x-β)^2|dx\)
\(=|a|\displaystyle\int_{α}^{β}(x-α)^2(x-β)^2dx\)
\(=|a|\displaystyle\int_{α}^{β}(x-α)^2\{(x-α)+α-β\}^2dx\)
\(=|a|\left\{\displaystyle\int_{α}^{β}(x-α)^4dx+(α-β)\displaystyle\int_{α}^{β}2(x-α)^3dx+(α-β)^2\displaystyle\int_{α}^{β}(x-α)^2dx\right\}\)
\(=|a|\left\{\left[\displaystyle\frac{(x-α)^5}{5}\right]_α^β-(β-α)\left[\displaystyle\frac{(x-α)^4}{2}\right]_α^β+(β-α)^2\left[\displaystyle\frac{(x-α)^3}{3}\right]_α^β\right\}\)
\(=|a|(β-α)^5(\displaystyle\frac{1}{5}-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3})\)
\(=\displaystyle\frac{|a|}{30}(β-α)^5\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積の最大・最小 back→接線と面積②