区間で関数の式が違う定積分の問題について見ていきます。
(例題1)
関数 \(y=f(x)\) のグラフは、座標平面で原点に関して点対称である。さらにこのグラフの \(x≦0\) の部分は、軸が\(y\)軸に平行で、点\((-\displaystyle\frac{1}{2},\displaystyle\frac{1}{4})\) を頂点とし、原点を通る放物線と一致している。このとき \(x=-1\) におけるこの関数のグラフの接線とこの関数のグラフによって囲まれる図形の面積を求めよ。
(解答)
\(x≦0\) の関数の方程式は、条件より
\(y=a(x+\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{4}\)
これが原点を通るから
\(0=\displaystyle\frac{1}{4}a+\displaystyle\frac{1}{4}\)
\(a=-1\)
よって
\(y=-(x+\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{4}\) (\(x≦0\))
これを原点に関して対称移動したグラフの方程式は、「\(x→-x\), \(y→-y\) 」として
\(-y=-(-x+\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{4}\)
よって、\(x>0\) における関数の方程式は
\(y=(x-\displaystyle\frac{1}{2})^2-\displaystyle\frac{1}{4}\) (\(x>0\))
展開してまとめると
\(f(x)=-x^2-x\) (\(x≦0\))
\(f(x)=x^2-x\) (\(x>0\))
また、\(x=-1\) における接線の方程式は
\(f(-1)=0\)
\(f'(x)=-2x-1\) より \(f'(-1)=1\) だから
\(y=x+1\)
\(x>0\)において、この接線と \(y=x^2-x\) の交点の\(x\)座標を求めると
\(x^2-x=x+1\)
\(x^2-2x-1=0\)
\(x=1±\sqrt{2}\)
\(x>0\)より \(x=1+\sqrt{2}\)
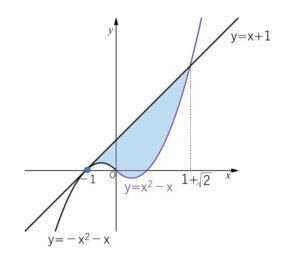
図より面積\(S\)は
\(S=\displaystyle\int_{-1}^{0}\{x+1-(-x^2-x)\}dx+\displaystyle\int_{0}^{1+\sqrt{2}}\{x+1-(x^2-x)\}dx\)
\(=\displaystyle\int_{-1}^{0}(x+1)^2dx+\displaystyle\int_{0}^{1+\sqrt{2}}(-x^2+2x+1)dx\)
\(=\left[\displaystyle\frac{(x+1)^3}{3}\right]_{-1}^{0}+\left[-\displaystyle\frac{x^3}{3}+x^2+x\right]_{0}^{1+\sqrt{2}}\)
\(=\displaystyle\frac{1}{3}-\displaystyle\frac{(1+\sqrt{2})^3}{3}+(1+\sqrt{2})^2+1+\sqrt{2}\)
\(=2+\displaystyle\frac{4\sqrt{2}}{3}\)
(例題2)
2つの関数
\(\begin{eqnarray} f(x) = \begin{cases} x & ( x ≦ 1 ) \\ 1 & ( x > 1 ) \end{cases} \end{eqnarray}\), \(g(x)=-x^2+ax+b\)
について、\(y=g(x)\) のグラフが、\(y=f(x)\) のグラフと2点で接するとき、
(1)\(a,b\)の値を求めよ。
(2)\(y=f(x)\) と \(y=g(x)\) のグラフで囲まれる部分の面積を求めよ。
(解答)
(1)
\(x>1\) の部分では、\(y=f(x)\) は\(x\)軸に平行な直線となっているので、放物線の頂点で接していて、
\(x≦1\) の部分では、放物線の左側の部分で接していることになります。
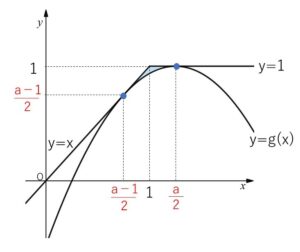
\(y=f(x)\) のグラフは2本の半直線を合わせたものだから、2点で接するためには
\(x≦1\), \(x>1\) の部分でそれぞれ1点ずつ接することになる。
\(x>1\) においては、\(y=f(x)=1\) のグラフは\(x\)軸に平行だから、放物線の頂点で接することになる。
\(g(x)=-(x-\displaystyle\frac{a}{2})^2+\displaystyle\frac{a^2}{4}+b\) より
\(\displaystyle\frac{a^2}{4}+b=1\)・・・①
かつ
\(\displaystyle\frac{a}{2}>1\)・・・②
\(x≦1\) においては、\(y=g(x)\) が \(y=f(x)=x\) に接するとき、接点の\(x\)座標を\(t\)とすれば
\(g'(t)=f'(t)(=1)\)・・・③
\(g(t)=f(t)(=t)\)・・・④
\(g'(x)=-2x+a\) と③から
\(-2t+a=1\)
\(t=\displaystyle\frac{a-1}{2}\)
④より
\(-(\displaystyle\frac{a-1}{2})^2+a\cdot\displaystyle\frac{a-1}{2}+b=\displaystyle\frac{a-1}{2}\)・・・⑤
また接点の\(x\)座標は、1以下なので
\(\displaystyle\frac{a-1}{2}≦1\)・・・⑥
①⑤の連立方程式を解いて、②⑥の不等式を満たすか確認していきます。
②より \(a>2\)
⑥より \(a≦3\)
つまり、\(2<a≦3\)
\(\displaystyle\frac{a^2}{4}+b=1\)・・・①
\(\displaystyle\frac{a^2}{4}-\displaystyle\frac{1}{2}a+b+\displaystyle\frac{1}{4}=0\)・・・⑤
①を⑤に代入して
\(1-\displaystyle\frac{1}{2}a+\displaystyle\frac{1}{4}=0\)
\(a=\displaystyle\frac{5}{2}\) (\(2<a≦3\)を満たす)
①より
\(b=-\displaystyle\frac{9}{16}\)
(2)
積分計算の際には、接していることから2つの関数の差をとると、\((x-t)^2\) の形になることに着目すると楽です。
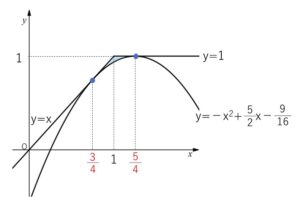
接点の\(x\)座標は
\(x=\displaystyle\frac{a-1}{2}=\displaystyle\frac{3}{4}\)
\(x=\displaystyle\frac{a}{2}=\displaystyle\frac{5}{4}\)
よって面積\(S\)は
\(S=\displaystyle\int_{\frac{3}{4}}^{1}\{x-(-x^2+\displaystyle\frac{5}{2}x-\displaystyle\frac{9}{16})\}dx+\displaystyle\int_{1}^{\frac{5}{4}}\{1-(-x^2+\displaystyle\frac{5}{2}x-\displaystyle\frac{9}{16})\}dx\)
\(=\displaystyle\int_{\frac{3}{4}}^{1}(x-\displaystyle\frac{3}{4})^2dx+\displaystyle\int_{1}^{\frac{5}{4}}(x-\displaystyle\frac{5}{4})^2dx\)
\(=\left[\displaystyle\frac{1}{3}(x-\displaystyle\frac{3}{4})^3\right]_{\frac{3}{4}}^{1}+\left[\displaystyle\frac{1}{3}(x-\displaystyle\frac{5}{4})^3\right]_{1}^{\frac{5}{4}}\)
\(=\displaystyle\frac{1}{3\cdot4^3}+\displaystyle\frac{1}{3\cdot4^3}\)
\(=\displaystyle\frac{1}{96}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→絶対値と積分① back→面積の最大・最小