軌跡・領域に関する面積の問題について見ていきます。
(例題)
実数\(t\)の値によって定まる \(P(t+1,t)\) と \(Q(t-1,-t)\) がある。\(t\)が閉区間 \([0,1]=\{t|0≦t≦1\}\) を動くとき、線分\(PQ\)が通過する範囲の面積を求めよ。
逆像法と順像法の2パターンで解いていきたいと思います。どちらもスタートは直線\(PQ\)の方程式を考えるところから始めます。
(解答1)逆像法
直線\(PQ\)の方程式は
\(y=\displaystyle\frac{t+t}{t+1-(t-1)}\{x-(t+1)\}+t\)
整理して
\(y=tx-t^2\)
(\(P\)の\(x\)座標)>(\(Q\)の\(x\)座標)より、線分\(PQ\)の方程式は次の通り。
\(y=tx-t^2\)・・・①
\(t-1≦x≦t+1\)・・・②
\(t\)が \(0≦t≦1\)・・・③ の範囲を動くときの、①②で表される線分\(PQ\)が通過する領域を求めたいので
\(t^2-xt+y=0\)・・・①’
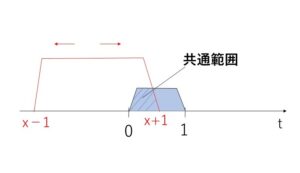
\(x-1≦t≦x+1\)・・・②’
\(0≦t≦1\)・・・③
とすると、\(t\)の2次方程式①’が、②’かつ③を満たす範囲に実数解をもつ条件を考えばよい。
(i)\(x<-1\) (共通範囲なし) (ii)\(-1≦x<0\) (iii)\(0≦x≦1\) (iv)\(1<x≦2\) (v)\(x>2\) (共通範囲なし) となります。
\(f(t)=t^2-xt+y\)
\(=(t-\displaystyle\frac{x}{2})^2-\displaystyle\frac{x^2}{4}+y\)
とおくと
(i)\(x<-1\) のとき
②’かつ③ を満たす\(t\)は存在しないので、①’の解は存在しないことになる。
よって、\(x<-1\) の領域は通過しない。
(ii)\(-1≦x<0\) のとき
②’かつ③ を満たす\(t\)の範囲は
\(0≦t≦x+1\)
\(f(t)\)の軸については
\(-\displaystyle\frac{1}{2}≦\displaystyle\frac{x}{2}<0\) (負の位置にある)
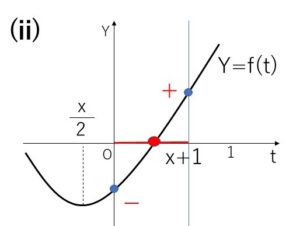
よって \(0≦t≦x+1\) に解をもつ条件は
\(f(0)≦0\) かつ \(f(x+1)≧0\)
\(y≦0\) かつ \((x+1)^2-(x+1)x+y≧0\)
したがって
\(y≦0\) かつ \(y≧-x-1\)
(iii)\(0≦x≦1\) のとき
②’かつ③ を満たす\(t\)の範囲は
\(0≦t≦1\)
\(f(t)\)の軸については
\(0≦\displaystyle\frac{x}{2}≦\displaystyle\frac{1}{2}\) (\(0≦t≦1\)の中間より左にある)
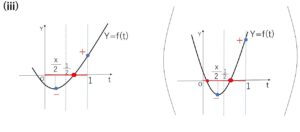
よって \(0≦t≦1\) に解をもつ条件は
\(D≧0\) かつ \(f(1)≧0\)
\(x^2-4y≧0\) かつ \(1-x+y≧0\)
したがって
\(y≦\displaystyle\frac{1}{4}x^2\) かつ \(y≧x-1\)
(iv)\(1<x≦2\) のとき
②’かつ③ を満たす\(t\)の範囲は
\(x-1≦t≦1\)
\(f(t)\)の軸については
\(\displaystyle\frac{1}{2}x=\displaystyle\frac{(x-1)+1}{2}\) (\(x-1≦t≦1\) のちょうど中間にある)
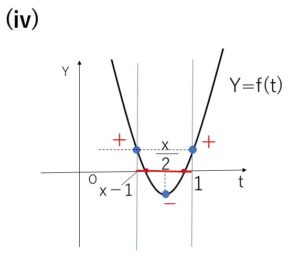
よって \(x-1≦t≦1\) に解をもつ条件は
\(D≧0\) かつ \(f(1)≧0\) (\(f(x-1)≧0\)でもよい)
\(x^2-4y≧0\) かつ \(1-x+y≧0\)
したがって
\(y≦\displaystyle\frac{1}{4}x^2\) かつ \(y≧x-1\)
(v)\(x>2\) のとき
②’かつ③ を満たす\(t\)は存在しないので、①’の解は存在しないことになる。
よって、\(x>2\) の領域は通過しない。
以上(i)~(v)をまとめると、次の不等式が表す領域が線分\(PQ\)の通過領域になる。
\(-x-1≦y≦0\) (\(-1≦x<0\))
\(x-1≦y≦\displaystyle\frac{1}{4}x^2\) (\(0≦x≦2\))
図示すると次の通り。
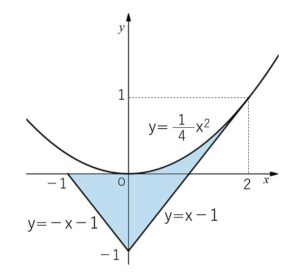
面積\(S\)は
\(S=\displaystyle\frac{1}{2}\cdot1\cdot1+\displaystyle\int_{0}^{2}\{\displaystyle\frac{1}{4}x^2-(x-1)\}dx\)
\(=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{4}\displaystyle\int_{0}^{2}(x-2)^2dx\)
\(=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{4}\left[\displaystyle\frac{(x-2)^3}{3}\right]_{0}^{2}\)
\(=\displaystyle\frac{1}{2}+\displaystyle\frac{2}{3}\)
\(=\displaystyle\frac{7}{6}\)
続いて順像法による解法です。途中までは逆像法の解法と同じです。
(解答2)順像法
\(P(t+1,t)\) \(Q(t-1,-t)\)
直線\(PQ\)の方程式は
\(y=\displaystyle\frac{t+t}{t+1-(t-1)}\{x-(t+1)\}+t\)
整理して
\(y=tx-t^2\)
(\(P\)の\(x\)座標)>(\(Q\)の\(x\)座標)より、線分\(PQ\)の方程式は次の通り。
\(y=tx-t^2\)・・・①
\(t-1≦x≦t+1\)・・・②
\(t\)が \(0≦t≦1\)・・・③ の範囲を動くときの、①②で表される線分\(PQ\)が通過する領域を求めたい。
動かす\(t\)の範囲は、②かつ③を満たす範囲になるのでこちらも共通範囲を同じように場合分けして考えることになります。
解答ではすべての実数\(x\) (\(=k\)) について考慮していきますが、点\(P\)の\(x\)座標が \(t+1\), \(Q\)の\(x\)座標が\(t-1\)で、\(0≦t≦1\) を\(t\)が動くので、線分\(PQ\)が「\(x<-1\), \(x>2\)の範囲を通過しない」のは明らかなので、最初から \(-1≦k≦2\) としても構いません。
ここで、\(x=k\) と固定して
\(y=f(t)=-t^2+kt\)・・・①’
\(k-1≦t≦k+1\)・・・②’
\(0≦t≦1\)・・・③
とすると、\(y=f(t)\) が、\(t\)が②’かつ③を満たす範囲で動くときのとりうる値を考えればよい。
\(f(t)=-(t-\displaystyle\frac{k}{2})^2+\displaystyle\frac{k^2}{4}\) より
(i)\(k<-1\) のとき
②’かつ③を満たす\(t\)は存在しないため、\(y\)のとりうる値はない。
(ii)\(-1≦k<0\) のとき
②’かつ③を満たす\(t\)の範囲は
\(0≦t≦k+1\)
\(y=f(t)\) の軸 \(t=\displaystyle\frac{k}{2}\) について
\(-\displaystyle\frac{1}{2}≦\displaystyle\frac{k}{2}<0\) と \(y=f(t)\)が上に凸の2次関数であることから
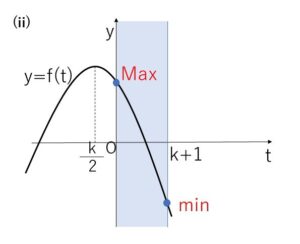
\(f(k+1)≦f(t)≦f(0)\)
\(-(k+1)^2+k(k+1)≦y≦0\)
よって
\(-k-1≦y≦0\)
(iii)\(0≦k≦1\) のとき
②’かつ③を満たす\(t\)の範囲は
\(0≦t≦1\)
\(y=f(t)\) の軸 \(t=\displaystyle\frac{k}{2}\) について
\(0≦\displaystyle\frac{k}{2}<\displaystyle\frac{1}{2}\) (\(0≦t≦1\) の中間より左側) より
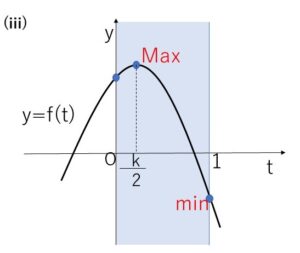
\(f(1)≦f(t)≦f(\displaystyle\frac{k}{2})\)
よって
\(-1+k≦y≦\displaystyle\frac{k^2}{4}\)
(iv)\(1<k≦2\) のとき
②’かつ③を満たす\(t\)の範囲は
\(k-1≦t≦1\)
\(y=f(t)\) の軸 について
\(\displaystyle\frac{k}{2}=\displaystyle\frac{(k-1)+1}{2}\) (\(k-1≦t≦1\) のちょうど中間にある)
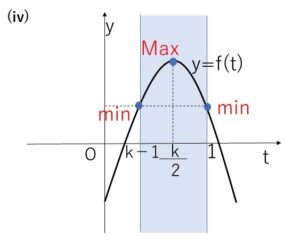
\(f(1)≦f(t)≦f(\displaystyle\frac{k}{2})\) (左辺は\(f(k-1)\)でもよい)
よって
\(-1+k≦y≦\displaystyle\frac{k^2}{4}\)
(v)\(k>2\) のとき
②’かつ③を満たす\(t\)は存在しないため、\(y\)のとりうる値はない。
以上(i)~(v) を\(k→x\) に戻してまとめると
\(-x-1≦y≦0\) (\(-1≦x<0\))
\(x-1≦y≦\displaystyle\frac{1}{4}x^2\) (\(0≦x≦2\))
(以下、図示と面積計算は(解答1)と同じなので省略)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円と曲線に囲まれた面積 back→対称な図形の面積