((注)この単元では因数の係数は有理数に限定します。)
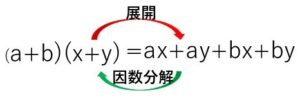
整式をいくつかの整式の積の形に表すことを因数分解といいます。つまり因数分解は展開の逆の操作です。展開は分配法則を使えば機械的に計算できるのに対して、因数分解は共通因数を見つけることが難しい場合があるため、工夫が必要になる場合が多いです。
(因数分解の基本)
共通因数をくくり出すことです。
共通因数をくくり出すことです。
(用語)
因数:一つの数や整式が、いくつかの数や整式の積の形で表されるときの、その個々の数や整式のこと。\(2ab\)の因数は、\(1,2,a,2b,ab\)などです。\(1\)や\(2ab\)そのものも因数に含めます。
因数:一つの数や整式が、いくつかの数や整式の積の形で表されるときの、その個々の数や整式のこと。\(2ab\)の因数は、\(1,2,a,2b,ab\)などです。\(1\)や\(2ab\)そのものも因数に含めます。
(例)
\(ab+ac-ad\)
\(=a(b+c-d)\)
\((x+1)-2y(x+1)\)
\(=(x+1)(1-2y)\)
工夫① 公式の暗記と利用
よくあるパターンを公式として暗記して、利用する方法です。因数分解の公式は展開の公式のちょうど真逆です。→展開の公式
2次の公式
① \(a^2+2ab+b^2=(a+b)^2\)
② \(a^2-2ab+b^2=(a-b)^2\)
③ \(a^2-b^2=(a+b)(a-b)\)
④ \(x^2+(a+b)x+ab=(x+a)(x+b)\)
⑤ \(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
⑥ \(a^2+b^2+c^2+2ab+2bc+2ca\)
\(=(a+b+c)^2\)
① \(a^2+2ab+b^2=(a+b)^2\)
② \(a^2-2ab+b^2=(a-b)^2\)
③ \(a^2-b^2=(a+b)(a-b)\)
④ \(x^2+(a+b)x+ab=(x+a)(x+b)\)
⑤ \(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
⑥ \(a^2+b^2+c^2+2ab+2bc+2ca\)
\(=(a+b+c)^2\)
3次の公式
⑦ \(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
⑧ \(a^3\color{red}{-}3a^2b+3ab^2\color{red}{-}b^3=(a-b)^3\)
⑨ \(a^3+b^3=(a+b)(a^2\color{red}{-}ab+b^2)\)
⑩ \(a^3-b^3=(a\color{red}{-}b)(a^2+ab+b^2)\)
⑪ \(a^3+b^3+c^3-3abc\)
\(=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
⑦ \(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
⑧ \(a^3\color{red}{-}3a^2b+3ab^2\color{red}{-}b^3=(a-b)^3\)
⑨ \(a^3+b^3=(a+b)(a^2\color{red}{-}ab+b^2)\)
⑩ \(a^3-b^3=(a\color{red}{-}b)(a^2+ab+b^2)\)
⑪ \(a^3+b^3+c^3-3abc\)
\(=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
⑪に関しては公式として覚えてもよいですし、→3次の因数分解の応用 の方法で導いてもよいです。
※ちなみに因数分解ではないですが、
(⑪の右辺)
\(=(a+b+c)\)
\(×\displaystyle\frac{1}{2}\{(a-b)^2+(b-c)^2+(c-a)^2\}\)
\(=(a+b+c)\)
\(×\displaystyle\frac{1}{2}\{(a-b)^2+(b-c)^2+(c-a)^2\}\)
と変形できることを知っておくと役に立つことがあります。
※⑨⑩の応用(n次式の場合)
nが奇数のとき
\(a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-・・・+a^2b^{n-3}-ab^{n-2}+b^{n-1})\)
↑ここは+ ↑+と-が入れ替わり
nが自然数のとき
\(a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+・・・+a^2b^{n-3}+ab^{n-2}+b^{n-1})\)
↑ここだけ- ↑あとは全部+
\(a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-・・・+a^2b^{n-3}-ab^{n-2}+b^{n-1})\)
↑ここは+ ↑+と-が入れ替わり
nが自然数のとき
\(a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+・・・+a^2b^{n-3}+ab^{n-2}+b^{n-1})\)
↑ここだけ- ↑あとは全部+
※スマホ閲覧の場合は横にスクロールして下さい。
以上です。お疲れ様でした。
ここまで読んで頂きありがとうございました。