内積に関する等式・不等式の証明問題について見ていきます。
(例題)次の等式・不等式を証明せよ。(\(\vec{a},\vec{b},\vec{c}\)は、平面上のベクトルとする)
(1)\(|\vec{a}+\vec{b}+\vec{c}|^2+|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\)\(=|\vec{a}+\vec{b}|^2+|\vec{b}+\vec{c}|^2+|\vec{c}+\vec{a}|^2\)
(2)\(|\vec{a}+\vec{b}+\vec{c}|^2≧3(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})\)
(3)\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\)
(解答)
(1)
(i)(左辺)-(右辺)=0 を示す。
(ii)(左辺の変形)=(右辺) or (左辺)=(右辺の変形) を示す。
(iii)(左辺の変形)=(右辺の変形) を示す。
です。これはベクトルを含む場合でも同じです。
(左辺)
\(=|\vec{a}+\vec{b}+\vec{c}|^2+|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\)
\(=(\vec{a}+\vec{b}+\vec{c})\cdot(\vec{a}+\vec{b}+\vec{c})+|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\)
\(=(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+2\vec{a}\cdot\vec{b}+2\vec{b}\cdot\vec{c}+2\vec{c}\cdot\vec{a})+|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\)
\(=2(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})\)
(右辺)
\(=|\vec{a}+\vec{b}|^2+|\vec{b}+\vec{c}|^2+|\vec{c}+\vec{a}|^2\)
\(=(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2)+(|\vec{b}|^2+2\vec{b}\cdot\vec{c}+|\vec{c}|^2)+(|\vec{c}|^2+2\vec{c}\cdot\vec{a}+|\vec{a}|^2)\)
\(=2(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})\)
よって
(左辺)=(右辺)
(2)
(左辺)-(右辺)
\(=|\vec{a}+\vec{b}+\vec{c}|^2-3(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})\)
\(=(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+2\vec{a}\cdot\vec{b}+2\vec{b}\cdot\vec{c}+2\vec{c}\cdot\vec{a})-3(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})\)
\(=|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2-\vec{a}\cdot\vec{b}-\vec{b}\cdot\vec{c}-\vec{c}\cdot\vec{a}\)
\(a^2,b^2,c^2\) をそれぞれ半分に分割して並び替えると
\((\displaystyle\frac{1}{2}a^2-ab+\displaystyle\frac{1}{2}b^2)+(\displaystyle\frac{1}{2}b^2-bc+\displaystyle\frac{1}{2}c^2)+(\displaystyle\frac{1}{2}c^2-ca+\displaystyle\frac{1}{2}a^2)≧0\)
あとはそれぞれ平方完成するだけです。
\(=(\displaystyle\frac{1}{2}|\vec{a}|^2-\vec{a}\cdot\vec{b}+\displaystyle\frac{1}{2}|\vec{b}|^2)+(\displaystyle\frac{1}{2}|\vec{b}|^2-\vec{b}\cdot\vec{c}+\displaystyle\frac{1}{2}|\vec{c}|^2)+(\displaystyle\frac{1}{2}|\vec{c}|^2-\vec{c}\cdot\vec{a}+\displaystyle\frac{1}{2}|\vec{a}|^2)\)
\(=\displaystyle\frac{1}{2}(|\vec{a}|^2-2\vec{a}\cdot\vec{b}+|\vec{b}|^2)+\displaystyle\frac{1}{2}(|\vec{b}|^2-2\vec{b}\cdot\vec{c}+|\vec{c}|^2)+\displaystyle\frac{1}{2}(|\vec{c}|^2-2\vec{c}\cdot\vec{a}+|\vec{a}|^2)\)
\(=\displaystyle\frac{1}{2}|\vec{a}-\vec{b}|^2+\displaystyle\frac{1}{2}|\vec{b}-\vec{c}|^2+\displaystyle\frac{1}{2}|\vec{c}-\vec{a}|^2\)\(≧0\)
よって (左辺)≧(右辺) より不等式は証明された。
等号は、\(\vec{a}-\vec{b}=\vec{0}\) かつ \(\vec{b}-\vec{c}=\vec{0}\) かつ \(\vec{c}-\vec{a}=\vec{0}\) のとき
つまり \(\vec{a}=\vec{b}=\vec{c}\) のとき成立。
(3)
ただし2乗の差を利用できるのは、どちらも\(0\)以上の場合(どちらも\(0\)以下であるときも不等号の入れ替わりに注意すればOK)です。
\(|\vec{a}+\vec{b}|\) と \(|\vec{a}|+|\vec{b}|\) はどちらも\(0\)以上なので特に注意することはないですが、\(|\vec{a}|-|\vec{b}|\) は負になる場合もあるので場合分けしていきます。
\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\) において
①\(|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\) について
両辺\(0\)以上なので、
\((|\vec{a}|+|\vec{b}|)^2-|\vec{a}+\vec{b}|^2≧0\)
を示せばよい。
\((|\vec{a}|+|\vec{b}|)^2-|\vec{a}+\vec{b}|^2\)
\(=(|\vec{a}|^2+2|\vec{a}||\vec{b}|+|\vec{b}|^2)-(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2)\)
\(=2(|\vec{a}||\vec{b}|-\vec{a}\cdot\vec{b})\)・・・(A)
ここで \(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときは、(A)=0 となるので不等式は成立。(このとき等号成立)
\(\vec{a}≠\vec{0}\) かつ \(\vec{b}≠\vec{0}\) のときはなす角を\(θ\)として
(A)\(=2(|\vec{a}||\vec{b}|-|\vec{a}||\vec{b}|\cosθ)\)
\(=2|\vec{a}||\vec{b}|(1-\cosθ)≧0\)
よって不等式は成立。等号は \(\cosθ=1\) つまり \(θ=0°\) のときで、\(\vec{a},\vec{b}\) が同じ向きのとき。
等号成立についてまとめると
「\(\vec{a}=\vec{0}\)」 または 「\(\vec{b}=\vec{0}\)」 または 「\(\vec{a},\vec{b}\) が同じ向き」
②\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|\) について
(ア)\(|\vec{a}|-|\vec{b}|<0\) のとき、明らかに不等式は成立
(イ)\(|\vec{a}|-|\vec{b}|≧0\) (\(|\vec{a}|≧|\vec{b}|\)・・・(※)) のとき、先ほどと同様に2乗の差を考えればよく
\(|\vec{a}+\vec{b}|^2-(|\vec{a}|-|\vec{b}|)^2\)
\(=(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2)-(|\vec{a}|^2-2|\vec{a}||\vec{b}|+|\vec{b}|^2)\)
\(=2(\vec{a}\cdot\vec{b}+|\vec{a}||\vec{b}|)\)・・・(B)
ここで、\(\vec{a}=\vec{0}\) のときは、(※)より \(\vec{b}=\vec{0}\) だから
\(\vec{b}=\vec{0}\) (\(\vec{a}\)は任意) の場合に含めてよく、このとき (B)=0 より 不等式は成立。(このとき等号成立)
さらに \(\vec{b}=\vec{0}\) のときは任意の\(\vec{a}\)について(※)も満たす。
\(\vec{a}≠\vec{0}\) かつ \(\vec{b}≠\vec{0}\) のときはなす角を\(θ\)として
(B)\(=2(|\vec{a}||\vec{b}|\cosθ+|\vec{a}||\vec{b}|)\)
\(=2|\vec{a}||\vec{b}|(1+\cosθ)≧0\)
よって不等式は成立。等号は \(\cosθ=-1\) つまり \(θ=180°\) のときで、\(\vec{a},\vec{b}\) が反対向きのとき。
等号成立についてまとめると
「\(\vec{b}=\vec{0}\)」 または 「\(\vec{a},\vec{b}\) が反対向き かつ \(|\vec{a}|≧|\vec{b}|\)」
(3)の補足1
①\(|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\) を利用して、
②\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|\) を示すこともできます。
①において \(\vec{a}→\vec{a}+\vec{b}\), \(\vec{b}=-\vec{b}\) と置き換えると
\(|(\vec{a}+\vec{b})+(-\vec{b})|≦|\vec{a}+\vec{b}|+|-\vec{b}|\) より
\(|\vec{a}|≦|\vec{a}+\vec{b}|+|\vec{b}|\)
よって
\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|\) となります。
等号成立については①においては
「\(\vec{a}=\vec{0}\)」 または 「\(\vec{b}=\vec{0}\)」 または 「\(\vec{a},\vec{b}\) が同じ向き」
だから、これらを同じように置き換えると
「\(\vec{a}+\vec{b}=\vec{0}\)」 または 「\(-\vec{b}=\vec{0}\)」 または 「\(\vec{a}+\vec{b},-\vec{b}\) が同じ向き」
となり、整理すると解答と同じ条件になります。
(3)の補足2
\(|\vec{a}|-|\vec{b}|≦|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\)
は三角不等式とよばれます。名前の通り三角形に関する不等式ですが、三角形の辺において (2辺の和)>(残りの1辺) という不等式が成り立つので、例題の不等式を図形的にとらえることもできます。等号成立のときは三角形ができない(つぶれてしまう)ときに対応します。
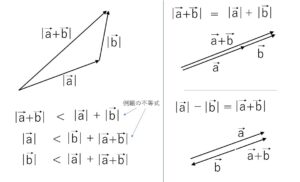
(3)の補足3
\(|\vec{b}|-|\vec{a}|≦|\vec{a}+\vec{b}|\) についても同様に成り立つので、より例題の不等式を一般化すると次の通りです。
\(||\vec{a}|-|\vec{b}||≦|\vec{a}+\vec{b}|≦|\vec{a}|+|\vec{b}|\)
(この不等式の証明自体は辺々がすべて\(0\)以上なので簡単です)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→内積と三角形の面積 back→内積とベクトルの大きさ②