2次関数の文章問題です。日本語で書かれた文章をうまく数式に翻訳します。
(問題)
一定の長さの針金を2つの部分に分け、その1つで円を、他の1つで正方形をつくる。つくった円と正方形の面積の和が最小となるのは、針金をどのような割合で分けるときか。
(解答)
針金全体の長さを \(l\) (定数) として、円をつくる針金の長さを \(x\) とすれば、正方形をつくる針金の長さは \(l-x\) 。どちらの図形も針金の長さが存在する、すなわち長さの値が正なので、\(x>0\) かつ \(l-x>0\)。 よって \(0<x<l\)・・・①
このとき、円の半径は \(\displaystyle\frac{x}{2\pi}\) 、正方形の1辺は\(\displaystyle\frac{l-x}{4}\)。円と正方形の面積の和を\(S\)とすれば
\(S=π(\displaystyle\frac{x}{2\pi})^2+(\displaystyle\frac{l-x}{4})^2\)
\(=\displaystyle\frac{1}{4\pi}x^2+\displaystyle\frac{1}{16}(l-x)^2\)
\(=(\displaystyle\frac{1}{4\pi}+\displaystyle\frac{1}{16})x^2-\displaystyle\frac{l}{8}x+\displaystyle\frac{l^2}{16}\)
\(=\displaystyle\frac{π+4}{16π}(x^2-\displaystyle\frac{2πl}{π+4}x)+\displaystyle\frac{l^2}{16}\)
\(=\displaystyle\frac{π+4}{16π}(x-\displaystyle\frac{πl}{π+4})^2-\displaystyle\frac{πl^2}{16(π+4)}+\displaystyle\frac{l^2}{16}\)
\(=\displaystyle\frac{π+4}{16π}(x-\displaystyle\frac{πl}{π+4})^2+\displaystyle\frac{l^2}{4(π+4)}\)・・・②
\(0<\displaystyle\frac{π}{π+4}<1\)から、
\(0<\displaystyle\frac{πl}{π+4}<l\)となり、②の2次関数について①の範囲内に軸があるのでグラフは下図のようになる。
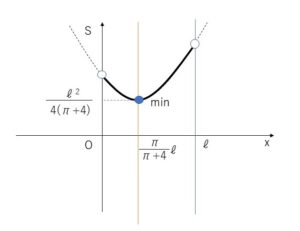
したがって、\(x=\displaystyle\frac{πl}{π+4}\)のとき\(S\)は最小となり、正方形の針金の長さは、\(l-x=l-\displaystyle\frac{πl}{π+4}=\displaystyle\frac{4l}{π+4}\)。
針金の長さの比は
\(x:l-x=\displaystyle\frac{πl}{π+4}:\displaystyle\frac{4l}{π+4}=\)\(π:4\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。