角の2等分線とベクトルについて見ていきます。
その後、角の2等分線のベクトル表記について解説します。
また三角形の内心(内接円の中心)は、内角の2等分線の交点になるので似たような考え方を使いますが、これについては次回に回したいと思います。
・角の2等分線と比
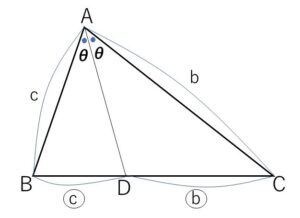
\(△ABC\)の\(\angle A\)の2等分線と辺\(BC\)との交点を\(D\)とすると
\(AB:AC=BD:DC\)
(簡単に証明すると)
補助線を引かない方法だと、三角形の面積を考えることになる。
\(△ABD:△ADC\)
\(=\displaystyle\frac{1}{2}AD \cdot AB\sinθ:\displaystyle\frac{1}{2}AD \cdot AC\sinθ\)
\(=AB:AC\)
また、この2つの三角形について底辺を\(BD,DC\)とみると高さは共通だから
\(△ABD:△ADC=BD:DC\)
よって
\(AB:AC=BD:DC\)
・角の2等分線のベクトル表記
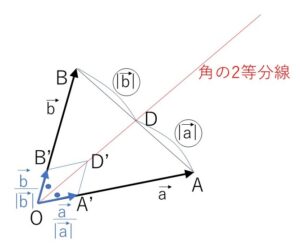
2つのベクトル、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) のなす角の2等分線について考えます。
三角形\(OAB\)において、角の2等分線と\(AB\)の交点を\(D\)とすれば
\(\overrightarrow{OD}=\displaystyle\frac{|\vec{b}|\cdot\vec{a}+|\vec{a}|\cdot\vec{b}}{|\vec{a}|+|\vec{b}|}=\displaystyle\frac{|\vec{a}||\vec{b}|}{|\vec{a}|+|\vec{b}|}\left(\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}\right)\)
角の二等分線上の点\(P\)は、\(\overrightarrow{OD}\) の実数倍を考えて
\(\overrightarrow{OP}=k\cdot\displaystyle\frac{|\vec{a}||\vec{b}|}{|\vec{a}|+|\vec{b}|}\left(\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}\right)\)
\(k\cdot\displaystyle\frac{|\vec{a}||\vec{b}|}{|\vec{a}|+|\vec{b}|}=t\) (実数の定数) とおくと
\(\overrightarrow{OP}=t\left(\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}\right)\) ・・・① (角の2等分線のベクトル表記)
ここで \(\overrightarrow{OA’}=\displaystyle\frac{\vec{a}}{|\vec{a}|}\), \(\overrightarrow{OB’}=\displaystyle\frac{\vec{b}}{|\vec{b}|}\) は、それぞれ\(\vec{a},\vec{b}\)と同じ向きの単位ベクトル(大きさ1のベクトル)だから、\(OA’,OB’\)を2辺とする平行四辺形\(OA’D’B’\)はひし形になります。
\(\overrightarrow{OA’}+\overrightarrow{OB’}=\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}=\overrightarrow{OD’}\)
であり、\(OD’\)はひし形の対角線であることと、ひし形の対角線は内角を2等分することから、上記①のベクトルが角の2等分線を表していることに納得がいきます。
また次のように2等辺三角形を考えてもよいでしょう。
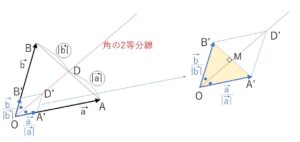
三角形\(OA’B’\)は2等辺三角形なので、角の2等分線と\(A’B’\)の交点\(M\)は\(A’B’\)の中点。
よって、角の2等分線上の点を\(P\)とすると
\(\overrightarrow{OP}=k\overrightarrow{OM}=k\cdot\displaystyle\frac{1}{2}\left(\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}\right)\)
\(\displaystyle\frac{1}{2}k=t\) とおけば
\(\overrightarrow{OP}=t\left(\displaystyle\frac{\vec{a}}{|\vec{a}|}+\displaystyle\frac{\vec{b}}{|\vec{b}|}\right)\)
(例題1)
\(△ABC\)において \(AB=4\), \(BC=2\), \(CA=3\) とする。\(\angle A\) の2等分線と\(BC\)の交点を\(D\)とするとき、\(\overrightarrow{AD}=□\overrightarrow{AB}+□\overrightarrow{AC}\) である。
また、\(\angle B\) の2等分線と\(AC\)の交点を\(E\)とし、\(AD\)と\(BE\)の交点を\(I\)とすると、\(\overrightarrow{AI}=□\overrightarrow{AD}\), \(\overrightarrow{BI}=□\overrightarrow{BE}\) である。
後半部分は交点のベクトルとして 「係数比較 や 係数の和=1」などを考えてもよいですが、比の定理だけでも解けます。
(解答)
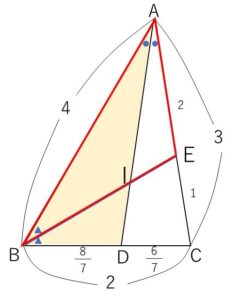
(前半)
\(BD:DC=4:3\) より
\(\overrightarrow{AD}=\displaystyle\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{4+3}\)
\(=\displaystyle\frac{3}{7}\overrightarrow{AB}+\displaystyle\frac{4}{7}\overrightarrow{AC}\)
(後半)
\(BD=2×\displaystyle\frac{4}{7}=\displaystyle\frac{8}{7}\)
\(△BDA\) において
\(AI:ID=BA:BD=4:\displaystyle\frac{8}{7}=7:2\)
よって
\(\overrightarrow{AI}=\displaystyle\frac{7}{9}\overrightarrow{AD}\)
また \(AE=3×\displaystyle\frac{4}{6}=2\)
\(△ABE\) において
\(BI:IE=AB:AE=4:2=2:1\)
よって
\(\overrightarrow{BI}=\displaystyle\frac{2}{3}\overrightarrow{BE}\)
(例題2)
図のように、中心\(O\)、半径\(1\)の円周上に相異なる3つの点\(B,C,D\)を
\(\angle BOC=\angle COD=θ\) (\(0°<θ<90°\))
となるようにとる。\(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とするとき、\(\overrightarrow{OD}\) を \(\vec{b},\vec{c},θ\) を用いて表せ。
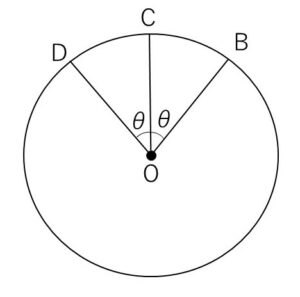
もしくは2等辺三角形\(OBD\)を考えて、\(OC\)上に\(BD\)の中点がある・・・としてもOKです。
(解答)
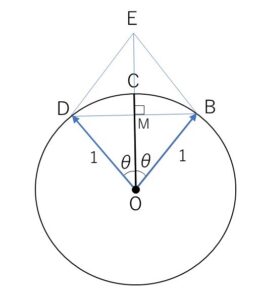
\(OB,OD\)を2辺とするひし形\(OBED\)を考える。
対角線\(OE\)上に\(C\)があるので
\(\overrightarrow{OE}=k\vec{c}\)・・・①
ひし形の2本の対角線の交点を\(M\)とすると、2本の対角線が直交することと、それぞれの対角線の中点が交点になることから
\(OE=2OM=2\cosθ\)
\(OC=1\) だから①の\(k\)は
\(k=2\cosθ\)
よって \(\overrightarrow{OE}=\vec{b}+\overrightarrow{OD}\) と①より
\(\vec{b}+\overrightarrow{OD}=(2\cosθ)\vec{c}\)
したがって
\(\overrightarrow{OD}=(2\cosθ)\vec{c}-\vec{b}\)
(例題3)
\(△OAB\)において、\(\vec{a}=\overrightarrow{OA}\), \(\vec{b}=\overrightarrow{OB}\) とする。\(|\vec{a}|=3\), \(|\vec{b}|=5\), \(\cos\angle AOB=\displaystyle\frac{3}{5}\) とする。このとき、\(\angle AOB\) の2等分線と、\(B\)を中心とする半径\(\sqrt{10}\)の円との交点の、\(O\)を原点とする位置ベクトルを、\(\vec{a},\vec{b}\) を用いて表せ。
\(\overrightarrow{OD}=\displaystyle\frac{5\vec{a}+3\vec{b}}{3+5}\)
求める交点の位置ベクトルは、\(\overrightarrow{OD}\)の実数倍です。
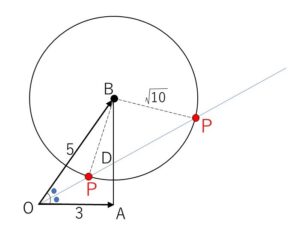
角の2等分線と\(AB\)の交点を\(D\)とすると
\(\overrightarrow{OD}=\displaystyle\frac{5\vec{a}+3\vec{b}}{3+5}=\displaystyle\frac{5}{8}\vec{a}+\displaystyle\frac{3}{8}\vec{b}\)
円と角の2等分線の交点を\(P(\vec{p})\) おけば
\(\vec{p}=k(\displaystyle\frac{5}{8}\vec{a}+\displaystyle\frac{3}{8}\vec{b})\)
またベクトルの大きさは2乗を考えて、内積におとします。
\(\overrightarrow{BP}=\overrightarrow{OP}-\overrightarrow{OB}\)
\(=k(\displaystyle\frac{5}{8}\vec{a}+\displaystyle\frac{3}{8}\vec{b})-\vec{b}\)
\(=\displaystyle\frac{5}{8}k\vec{a}+(\displaystyle\frac{3}{8}k-1)\vec{b}\)
\(|\overrightarrow{BP}|^2=10\) より
\(\left|\displaystyle\frac{5}{8}k\vec{a}+(\displaystyle\frac{3}{8}k-1)\vec{b}\right|^2=10\)
\(\displaystyle\frac{25}{64}k^2|\vec{a}|^2+2\cdot\displaystyle\frac{5}{8}k(\displaystyle\frac{3}{8}k-1)\vec{a}\cdot\vec{b}+(\displaystyle\frac{3}{8}k-1)^2|\vec{b}|^2=10\)
\(|\vec{a}|=3\), \(|\vec{b}|=5\)
\(\vec{a}\cdot\vec{b}=3\cdot5\cdot\displaystyle\frac{3}{5}=9\) より
\(\displaystyle\frac{25}{64}k^2\cdot9+2\cdot\displaystyle\frac{5}{8}k(\displaystyle\frac{3}{8}k-1)\cdot9+(\displaystyle\frac{3}{8}k-1)^2\cdot25=10\)
整理すると
\(3k^2-8k+4=0\)
\((3k-2)(k-2)=0\)
\(k=\displaystyle\frac{2}{3},2\)
したがって
\(\vec{p}=k(\displaystyle\frac{5}{8}\vec{a}+\displaystyle\frac{3}{8}\vec{b})\) より
\(\vec{p}=\displaystyle\frac{5}{12}\vec{a}+\displaystyle\frac{1}{4}\vec{b}\), \(\vec{p}=\displaystyle\frac{5}{4}\vec{a}+\displaystyle\frac{3}{4}\vec{b}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の内接円とベクトル back→交点の位置ベクトル①