軌跡・領域⑤(ベクトルの選択)

問題文にベクトルの記述がない場合で、ベクトルを用いて解く図形問題について見ていきます。

まず少しだけ問題を解く方針についてまとめておきます。
図形問題が与えられたときに、問題文に解法の方針が無い場合大きく分けて次の解法が考えられます。(もしくは方針があっても敢えて他の方針にしてもよい)
(1)座標で解く (2)ベクトルで解く (3)幾何で解く
今回の例題では(2)の手法を選ぶものを扱っていきます。

(例題1)
1辺の長さが\(1\)の正六角形\(ABCDEF\)が与えられている。点\(P\)が辺\(AB\)上を、点\(Q\)が辺\(CD\)上をそれぞれ独立に動くとき、線分\(PQ\)を\(2:1\)に内分する点\(R\)が通りうる範囲の面積を求めよ。

解法の方針が与えられていないので、どの手法をとるかをまず考えます。
正六角形の辺についてなので、座標で考えると、辺の方程式をたてて内分する点を求めて(媒介変数で表される)そこから軌跡を求めて・・・となりますが面倒そうです。よって辺の平行性や、内分と相性のいいベクトルを選択することになります。
この解法の選択をしてしまえば、あとはそれほど難しい問題ではありません。

(解答)

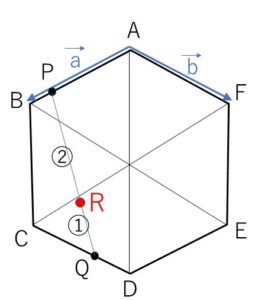
ベクトル領域⑤ 例題1-1

\(\overrightarrow{AB}=\vec{a}\),　\(\overrightarrow{AF}=\vec{b}\) とおく。

実数\(s,t\)を用いると
\(\overrightarrow{AP}=s\vec{a}\)　(\(0≦s≦1\))

\(\overrightarrow{AQ}=\overrightarrow{AC}+t\vec{b}\)　(\(0≦t≦1\))

\(\overrightarrow{AC}=2\vec{a}+\vec{b}\) ですが、\(\overrightarrow{AC}\)のままにしておきます。(どちらでもよい)

よって
\(\overrightarrow{AR}\)
\(=\displaystyle\frac{\overrightarrow{AP}+2\overrightarrow{AQ}}{2+1}\)
\(=\displaystyle\frac{2}{3}\overrightarrow{AC}+\displaystyle\frac{1}{3}s\vec{a}+\displaystyle\frac{2}{3}t\vec{b}\)

あとは図示するだけです。
\(\displaystyle\frac{2}{3}\overrightarrow{AC}\)が定ベクトルで、残りの部分が\(s,t\)が変化することで平行四辺形の内部を描きます。
図はそれほど正確に描く必要はありませんが、面積を求めるので辺の長さやなす角は求めておきます。

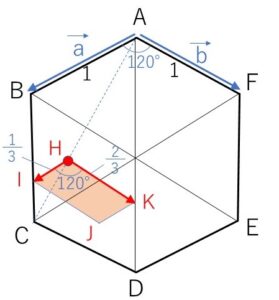
ベクトル領域⑤ 例題1-2

\(\displaystyle\frac{2}{3}\overrightarrow{AC}=\overrightarrow{AH}\) とすると

\(\overrightarrow{AR}=\overrightarrow{AH}+\displaystyle\frac{1}{3}s\vec{a}+\displaystyle\frac{2}{3}t\vec{b}\) より

\(0≦s,t≦1\) で\(s,t\)を動かすことにより、\(R\)は2辺が\(\displaystyle\frac{1}{3},\displaystyle\frac{2}{3}\)でなす角が\(120°\)の図の平行四辺形\(HIJK\)の周および内部を動く。

したがって面積\(S\)は
\(S=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{3}\cdot\displaystyle\frac{2}{3}\sin120°×2\)
\(=\displaystyle\frac{\sqrt{3}}{9}\)

(例題2)
三角形\(ABC\)に対し、辺\(AB\)上に点\(P\)を、辺\(BC\)上に点\(Q\)を、辺\(CA\)上に点\(R\)を、頂点とは異なるようにとる。この3点がそれぞれの辺上を動くとき、この3点を頂点とする三角形の重心はどのような範囲を動くか図示せよ。

同様にベクトルを選択します。領域を考えるとき\(P,Q,R\)の3つが動点なので1つを固定する必要がありますが、解答では \(A\)を基準として \(\overrightarrow{AB},\overrightarrow{AC}\) の2つのベクトルで考えるために、これと平行でない仲間外れの\(BC\)上の\(Q\)を固定します。

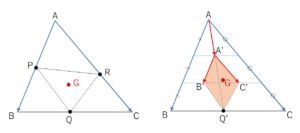
ベクトル領域⑤ 例題2-1

\(△PQR\)の重心を\(G\)とすると

\(\overrightarrow{AG}=\displaystyle\frac{1}{3}(\overrightarrow{AP}+\overrightarrow{AQ}+\overrightarrow{AR})\)

ここで\(BC\)上の\(Q\)をある点\(Q’\)に固定して、実数\(s,t\)を用いると
\(\overrightarrow{AG}=\displaystyle\frac{1}{3}(\overrightarrow{AP}+\overrightarrow{AQ’}+\overrightarrow{AR})\)
\(=\displaystyle\frac{1}{3}\overrightarrow{AQ’}+\displaystyle\frac{1}{3}s\overrightarrow{AB}+\displaystyle\frac{1}{3}t\overrightarrow{AC}\)　(\(0<s<1\),　\(0<t<1\))

と表せる。\(BC\)に平行な3等分線に注意すると、\(s,t\)を動かすことにより\(G\)は辺が\(AB\)と\(AC\)に平行な、図の平行四辺形\(A’B’Q’C’\)の内部(周を除く)を動く。

そして\(Q’\)を動かすことにより、平行四辺形は\(BC\)方向に平行移動するので、求める\(G\)の動く範囲を図示すると次の通り。

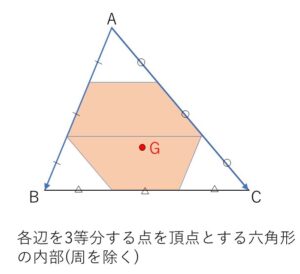
ベクトル領域⑤ 例題2-3

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の形状　 back→軌跡・領域④(等式・幾何の利用)