空間座標について見ていきます。
・空間座標
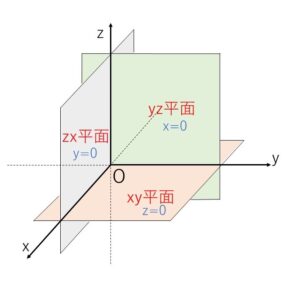
空間の座標は、原点\(O\)を通り互いに直交する3本の座標軸によって定められます。
これらの軸を\(x\)軸,\(y\)軸,\(z\)軸といい、\(x\)軸と\(y\)軸によって定められる平面を\(xy\)平面といい、慣れ親しんだ平面となります。同様に、\(y\)軸と\(z\)軸によって定められる平面を\(yz\)平面、\(z\)軸と\(x\)軸によって定めれられる平面を\(zx\)平面とよび、この3つの平面をまとめて座標平面とよびます。
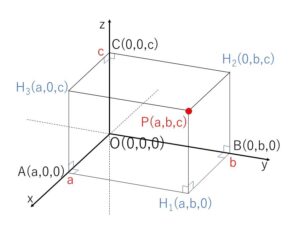
空間における点\(P\)において、この点を通り\(x\)軸,\(y\)軸,\(z\)軸に垂直な平面を考えて、これらの平面と\(x\)軸,\(y\)軸,\(z\)軸との交点をそれぞれ\(A,B,C\)とし、\(A,B,C\)の\(x\)軸,\(y\)軸,\(z\)軸に関する座標を\(a,b,c\)とします。すると空間における\(P\)に対して、実数\((a,b,c)\)の組がただ1つ定まることになり、また逆に\((a,b,c)\)の組を定めれば、\(P\)の位置がただ1つ定まることになります。そこでこの \((a,b,c)\) を点\(P\)の座標とし、\(a,b,c\)それぞれを、\(x\)座標,\(y\)座標,\(z\)座標といい、このように座標の定められた空間を座標空間といいます。
また、\(P(a,b,c)\)を通り\(xy\)平面に垂直な直線と\(xy\)平面との交点を\(H_1\)とします。このとき直線\(PH_1\)を\(P\)から\(xy\)平面に下ろした垂線、点\(H_1\)を垂線の足といいます。\(H_1\)の座標については、\(P\)と\(x,y\)座標が同じで\(z\)座標は\(0\)となるので\(H_1(a,b,0)\)となります。同様に\(yz\)平面、\(zx\)平面に下ろした垂線の足\(H_2,H_3\)も考えることができます。
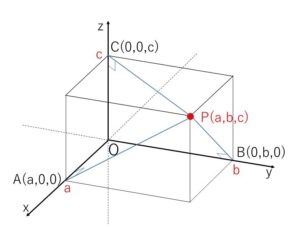
今度は軸に垂直な場合を考えます。\(P(a,b,c)\)を通り\(x\)軸に垂直な直線と\(x\)軸との交点は点\(A\)であり、直線\(PA\)を\(x\)軸に下した垂線、点\(A\)を垂線の足といいます。同様に\(y\)軸に下した垂線の足は\(B\)、\(z\)軸に下した垂線の足は\(C\)になります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間座標と対称