空間における対称な点に関する知識について整理していきます。
・空間座標と対称な点
まずは軸について対称な点から考えます。
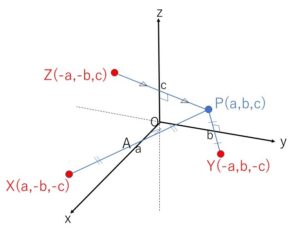
空間にある点\(P(a,b,c)\)から\(x\)軸に下した垂線の足を\(A\)として、直線\(AP\)上にある \(AP=AX\) を満たす\(P\)でない点を\(X\)とするとき、点\(P\)と点\(X\)は\(x\)軸に関して対称であるといいます。このとき、\(X\)の\(x\)座標は\(P\)と同じで\(y,z\)座標は符号が反対になるので、\(X(a,-b,-c)\) となります。同様に\(y\)軸に関して対称な点の座標は\(Y(-a,b,-c)\)、\(z\)軸に関して対称な点の座標は\(Z(-a,-b,c)\)です。
次に平面について対称な点について考えます。
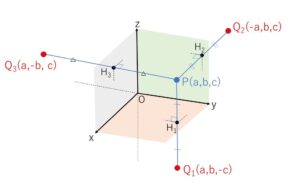
点\(P\)から\(xy\)平面に下した垂線の足を\(H_1\)とし、直線\(PH_1\)上にある\(H_1P=H_1Q_1\) を満たす\(P\)でない点を\(Q_1\)とするとき、点\(P\)と点\(Q_1\)は\(xy\)平面に関して対称であるといいます。このとき、\(Q_1\)の\(x,y\)座標は\(P\)と同じで\(z\)座標は符号が反対になるので、\(Q_1(a,b,-c)\) となります。同様に\(yz\)平面に関して対称な点の座標は\(Q_2(-a,b,c)\)、\(zx\)平面に関して対称な点の座標は\(Q_3(a,-b,c)\)です。
ちょうど平面を鏡に見立てると、点\(P\)とその像\(Q_1,Q_2,Q_3\)が対称な関係です。
最後に原点に対称な点を考えます。
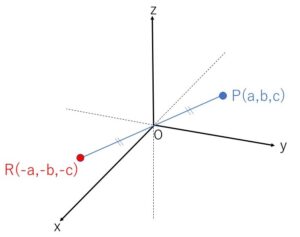
直線\(PO\)上にある\(OP=OR\)を満たす\(P\)でない点を\(R\)とするとき、点\(P\)と点\(R\)は原点に関して対称であるといいます。\(R\)の座標は\(P\)の座標の符号を入れ替えたものになるので、\(R(-a,-b,-c)\)です。
(例題)
点\(P\)を\(xy\)平面に関して対称移動し、さらに\(y\)軸に関して対称移動すると、座標が\((2,1-3)\)になった。点\(P\)の座標を求めよ。
のどちらかの方法になります。解答では②で解きたいと思います。
(解答)
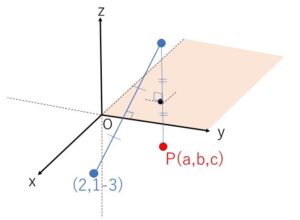
\((2,1-3)\) を\(y\)軸について対称移動させると、\((-2,1,3)\)
さらに \(xy\)平面について対称移動させると、\((-2,1,-3)\)
したがって \(P(-2,1,-3)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間における距離 back→空間座標の基礎