空間における距離は、三平方の定理を2回使うことで求めることができます。
・空間における距離
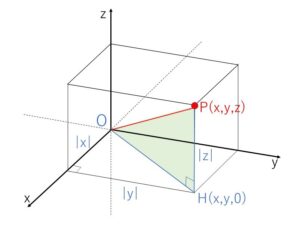
まず、原点\(O(0,0,0)\) と 点\(P(x,y,z)\) の距離について考えます。
\(P\)から\(xy\)平面に下ろした垂線の足を\(H\)とすると\(H(x,y,0)\)であり、\(xy\)平面上の直角三角形より
\(OH^2=x^2+y^2\)
また直角三角形\(PHO\)より
\(OP^2=OH^2+HP^2=x^2+y^2+z^2\)
したがって
\(OP=\sqrt{x^2+y^2+z^2}\)
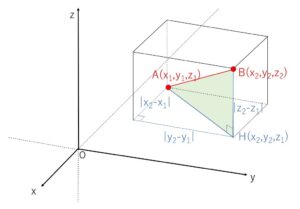
次に2点 \(A(x_1,y_1,z_1)\), \(B(x_2,y_2,z_2)\) の距離は、図より上の内容を
\(x→x_2-x_1\), \(y→y_2-y_1\), \(z→z_2-z_1\) と置き換えればよいので
\(AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\)
\(AB=\sqrt{x^2+y^2+z^2}(=OB)\)
となるので、\(AB\)についての公式のほうがより一般的なものになります。
(例題1)
3点 \(A(-1,0,1)\), \(B(1,-1,3)\), \(C(0,2,1)\) を頂点とする三角形\(ABC\)はどのような形か。
等しい辺を探したり、三平方の定理の逆を使うために辺の長さを調べます。
(解答)
\(AB^2=(1+1)^2+(-1-0)^2+(3-1)^2=9\)
\(BC^2=(0-1)^2+(2+1)^2+(1-3)^2=14\)
\(CA^2=(0+1)^2+(2-0)^2+(1-1)^2=5\)
よって
\(CA^2+AB^2=BC^2\) が成り立つので
\(\angle A=90°\) の直角三角形
(例題2)
空間に相異なる4点 \(O(0,0,0)\), \(A(a,0,0)\), \(B(0,b,0)\), \(C(c,c,c)\) がある。ただし\(a,b\)は正の数とする。4点 \(O,A,B,C\) への距離がいずれも相等しい 点\(P(x,y,z)\) が\(xy\)平面に関して\(C\)と同じ側(\(xy\)平面上は除く)にあるのは、\(a,b,c\)にどのような関係があるときか。
(解答)
以下 \(a>0\), \(b>0\) と 4点が異なるから \(c≠0\) に注意する。
\(OP^2=AP^2=BP^2=CP^2\) より
\(x^2+y^2+z^2=(x-a)^2+y^2+z^2\)
\(=x^2+(y-b)^2+z^2=(x-c)^2+(y-c)^2+(z-c)^2\)
\(OP^2=AP^2\), \(OP^2=BP^2\), \(OP^2=CP^2\) を整理すると
\(2ax=a^2\), \(2by=b^2\), \(2c(x+y+z)=3c^2\)
\(a,b,c\)は\(0\)でないから
\(x=\displaystyle\frac{a}{2}\)・・・①
\(y=\displaystyle\frac{b}{2}\)・・・②
\(x+y+z=\displaystyle\frac{3}{2}c\)・・・③
①②を③に代入して整理すると
\(z=\displaystyle\frac{-a-b+3c}{2}\)・・・③’
\(z\)座標の符号が同じであればよいので、\(zc>0\) です。
\(P\)と\(C\)が\(xy\)平面に関して同じ側にあるので
\(zc>0\)・・・④
③’を④に代入して
\(\displaystyle\frac{-a-b+3c}{2}×c>0\)
「\(c\)の2次不等式」と見てもよいですし、「正×正 or 負×負」 と考えてもよいです。
\(c(c-\displaystyle\frac{a+b}{3})>0\)
\(a+b>0\) だから求める関係式は
\(c<0\) または \(c>\displaystyle\frac{a+b}{3}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→空間ベクトルの定義と演算 back→空間座標と対称