\(\require{cancel}\)
空間ベクトルにおける1次独立について見ていきます。
空間ベクトルの1次独立の話に入る前に、空間において2つのベクトルが平面を描くことについて軽く触れておきます。
・2つのベクトルが描く平面
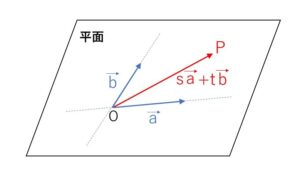
\(\vec{0}\)でなく、平行でない2つのベクトル\(\vec{a},\vec{b}\)について、2つのベクトルの始点を合わせます。始点\(O\)を通り2つのベクトル方向の2本の直線を考えると、交わる2つの直線を含む平面が決定します。この平面は2本の直線の一方を他方に沿って平行移動することでできる平面なので、2本の直線方向を2つの軸として考えると
\(\overrightarrow{OP}=s\vec{a}+t\vec{b}\)・・・① (\(s,t\)は実数)
で表される\(P\)はこの平面上(\(\vec{a},\vec{b}\)で作られる平面上)に存在することが分かります。
もしくは、\(\vec{a},\vec{b}\)で作られる平面が\(xy\)平面になるように\(x,y,z\)軸を設定し座標空間を考えると、\(\vec{a}=(a_1,a_2,0)\), \(\vec{b}=(b_1,b_2,0)\) とおけるので、①で表される\(P\)は\(xy\)平面上にあると考えることもできます。
また平面ベクトルのときと同様に、この平面上の任意の点\(P\)について①の形で表すことができ、その表し方は1通りです。
・1次独立(空間)
空間では、3つのベクトルを主役に考えていきます。
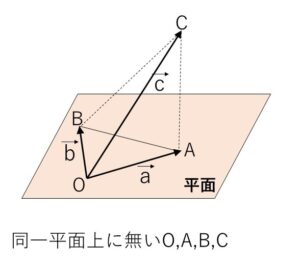
空間におけるベクトル \(\vec{a},\vec{b},\vec{c}\) のうち、1つのベクトルが残りのベクトルの実数倍の和(1次結合)で表されるとき、これらのベクトルの組は1次従属といい、 \(\vec{a},\vec{b},\vec{c}\) のどのベクトルも残りのベクトルの実数倍の和で表すことができない場合、これらのベクトルの組は1次独立であるといいます。
空間における1次独立について次のことが成り立ちます。
\(\vec{a},\vec{b},\vec{c}\) が1次独立 \(⇔\) \(\vec{a},\vec{b},\vec{c}\) が同一平面上にない
空間ベクトルではこの同一平面上にないということがポイントになります。\(\vec{0}\)でないことと平行でないことはこの条件だけで保証されます。
(解説)
(\(→\) について)
まず\(\vec{a}=\vec{0}\)とすると、例えば \(\vec{a}=0×\vec{b}\) と表されるので矛盾。
よって、\(\vec{a}≠\vec{0}\)
同様に、\(\vec{b}≠\vec{0}\), \(\vec{c}≠\vec{0}\)
また、\(\vec{a}/\!/\vec{b}\) とすると、\(\vec{a}=k\vec{b}\) と表されるので矛盾。
\(\vec{a}\bcancel{/\!/}\vec{b}\)
同様に、\(\vec{b}\bcancel{/\!/}\vec{c}\), \(\vec{c}\bcancel{/\!/}\vec{a}\)
そして\(O,A,B,C\)が同一平面上にあるすると、例えば
\(\vec{c}=s\vec{a}+t\vec{b}\) と表されるので矛盾。
したがって、\(\vec{a},\vec{b},\vec{c}\) は同一平面上にない。
(\(←\)について)
\(O,A,B,C\)が同一平面上にないので、\(\vec{a},\vec{b},\vec{c}\) は \(\vec{0}\)でない。(例えば\(\vec{a}=\vec{0}\)とすると、\(O(A),B,C\)の3点を通る平面があり矛盾)
また、\(\vec{a},\vec{b},\vec{c}\)はどの2つも平行でない。
(例えば\(\vec{a}/\!/\vec{b}\)とすると、\(O,A,B\)が一直線上にあるので、この直線と\(C\)を含む平面があり矛盾)
そして、\(O,A,B,C\)が同一平面上にないので
\(\vec{a}=s_1\vec{b}+t_1\vec{c}\)
\(\vec{b}=s_2\vec{c}+t_2\vec{a}\)
\(\vec{c}=s_3\vec{a}+t_3\vec{b}\)
を満たす\(s_1~s_3,t_1~t_3\) が存在しない。
したがって、\(\vec{a},\vec{b},\vec{c}\) は1次独立。
・一意性・任意性
空間ベクトルにおいても、\(\vec{a},\vec{b},\vec{c}\) が1次独立のとき次のことが成り立ちます。
(1)任意の空間ベクトル\(\vec{p}\)は、\(\vec{a},\vec{b},\vec{c}\) で表せる。
(2)その表し方は1通りしかない
(解説)
\(\vec{p}=\overrightarrow{OP}\), \(\vec{a}=\overrightarrow{OA}\), \(\vec{b}=\overrightarrow{OB}\), \(\vec{c}=\overrightarrow{OC}\) とする。
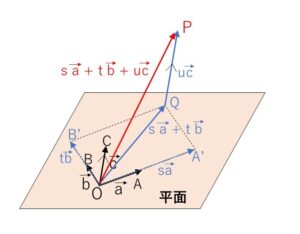
3点\(O,A,B\)を通る平面を\(α\)とする。点\(P\)から\(OC\)に平行な直線をひき、平面\(α\)との交点を\(Q\)とする。
\(Q\)は平面\(α\)上の点だから、実数\(s,t\)を用いて
\(\overrightarrow{OQ}=s\vec{a}+t\vec{b}\)
と表すことができる。また\(QP\)と\(OC\)が平行であるから実数\(u\)を用いて
\(\overrightarrow{QP}=u\vec{c}\)
と表せる。
よって
\(\vec{p}\)\(=\overrightarrow{OQ}+\overrightarrow{QP}\)
\(=s\vec{a}+t\vec{b}+u\vec{c}\)
と表せる。
そして、\(P\)から引いた\(OC\)に平行な直線と平面\(α\)との交点が\(Q\)であり、
\(s,t\)を変化させた実数倍の和 \(s’\vec{a}+t’\vec{b}\) は \(Q\)以外の点を表すので
\(s’\vec{a}+t’\vec{b}+k\vec{c}\) で\(k\)の値を変化させても\(\overrightarrow{OP}\)を表すことはできない。
したがって、\(\vec{p}\)の表し方は1通りになる。
・(係数)=0 と一意性
空間ベクトルにおいても次のことが成り立ちます。
\(\vec{a},\vec{b},\vec{c}\)が1次独立 \(⇔\) (I)を満たすのは \(s=t=u=0\) に限る
(解説)
(\(→\)について)
\(s≠0\) とすると(I)は
\(\vec{a}=-\displaystyle\frac{t}{s}\vec{b}-\displaystyle\frac{u}{s}\vec{c}\)
となり、1次独立であることに矛盾。よって\(s=0\)
同様に、\(t=0\), \(u=0\) となり、(I)を満たすのは\(s=t=u=0\)に限る。
(\(←\)について)
\(\vec{a},\vec{b},\vec{c}\) が1次独立でないとする。
例えば\(\vec{a}\)が残りの\(\vec{b},\vec{c}\)で表すことができる場合は
\(\vec{a}=k_1\vec{b}+k_2\vec{c}\) となり
\(\vec{a}-k_1\vec{b}-k_2\vec{c}=\vec{0}\) となるので、\(s=1\)が(I)を満たすので矛盾。
\(\vec{b},\vec{c}\)についても同じことが言えるので
\(\vec{a},\vec{b},\vec{c}\) は1次独立になる。
そして上記定理により次のことが成り立ちます。
\(\vec{a},\vec{b},\vec{c}\) が1次独立であるとき
\(s\vec{a}+t\vec{b}+u\vec{c}=s’\vec{a}+t’\vec{b}+u’\vec{c}\) であるとき、
\(s=s’\) かつ \(t=t’\) かつ \(u=u’\)
(証明)
\(s\vec{a}+t\vec{b}+u\vec{c}=s’\vec{a}+t’\vec{b}+u’\vec{c}\) より
\((s-s’)\vec{a}+(t-t’)\vec{b}+(u-u’)\vec{c}=\vec{0}\)
\(s-s’=0\), \(t-t’=0\), \(u-u’=0\) より
\(s=s’\), \(t=t’\), \(u=u’\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間ベクトルの内積 back→空間ベクトルと平行