三角形の面積

空間における三角形の面積公式は平面の場合と同様です。

・ベクトルと三角形の面積

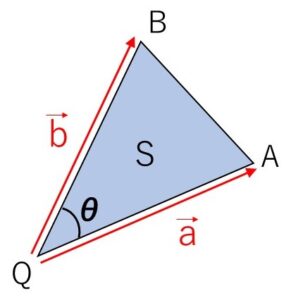
\(△QAB\) において、\(\overrightarrow{QA}=\vec{a}\),　\(\overrightarrow{QB}=\vec{b}\),　\(\angle AQB=θ\)　(\(0°<θ<180°\))　とする。

\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\) と  \(\sinθ>0\) より

\(\sin \theta=\sqrt{1-\left(\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\right)^2}=\displaystyle\frac{\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}{|\vec{a}||\vec{b}|}\)

\(S=\displaystyle\frac{1}{2}|\vec{a}||\vec{b}|\sinθ\) より

\(S=\displaystyle\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}\)・・・①  (ベクトル表記の面積公式)

(例題)
\(A(0,0,1)\), \(B(0,1,0)\) \(P(1,t,0)\) とする。\(△ABP\)の面積を\(t\)を用いて表せ。また、\(0≦t≦2\) のとき、その面積の最大値\(M\)、最小値\(m\)を求めよ。

(解答)

\(\overrightarrow{AB}=(0,1,-1)\)
\(\overrightarrow{AP}=(1,t,-1)\)

よって三角形の面積\(S\)は
\(S=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AP}|^2-(\overrightarrow{AB}\cdot\overrightarrow{AP})^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{(0+1+1)(1+t^2+1)-(0+t+1)^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{2t^2+4-(t^2+2t+1)}\)
\(=\displaystyle\frac{1}{2}\sqrt{t^2-2t+3}\)

また
\(\displaystyle\frac{1}{2}\sqrt{t^2-2t+3}\)
\(=\displaystyle\frac{1}{2}\sqrt{(t-1)^2+2}\)

\(0≦t≦2\) において

最大値は \(t=0,2\) のとき \(M=\displaystyle\frac{\sqrt{3}}{2}\)

最小値は \(t=1\) のとき \(m=\displaystyle\frac{\sqrt{2}}{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルのなす角、垂直なベクトル　back→空間ベクトルの内積