直線の方程式

空間における直線の表し方について見ていきます。

・直線のベクトル方程式(方向ベクトル表記)

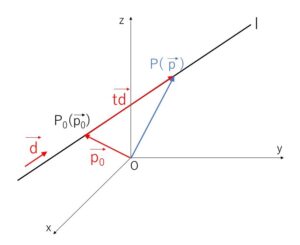
定点\(P_0(\vec{p_0})\)を通り、\(\vec{0}\)でないベクトル\(\vec{d}\)に平行な直線を\(l\)とします。
この直線上\(l\)の点を\(P(\vec{p})\)とすると、\(\overrightarrow{P_0P}/\!/\vec{d}\) または \(\overrightarrow{P_0P}=\vec{0}\) だから
\(\overrightarrow{P_0P}=t\vec{d}\)　(\(t\)は実数)
よって
\(\vec{p}-\vec{p_0}=t\vec{d}\)

\(\vec{p}=\vec{p_0}+t\vec{d}\)・・・①　(方向ベクトルによる直線の方程式)

①において、\(t\)がすべての実数値をとって変化すると点\(P(\vec{p})\)は直線\(l\)上のすべての点を動くので①が直線\(l\)を表していることになります。そこで①を直線\(l\)のベクトル方程式とよびます。また直線\(l\)の方向を決める\(\vec{d}\)のようなベクトルを方向ベクトルとよびます。

ここでベクトル方程式①を成分表示にしてみます。

\(P(x,y,z)\), \(P_0(x_0,y_0,z_0)\), \(\vec{d}=(a,b,c)\) として、位置ベクトルの基準を原点\(O\)とすれば①は

\((x,y,z)=(x_0,y_0,z_0)+t(a,b,c)\)

よって成分を比較すると

\(x=x_0+at\)・・・②
\(y=y_0+bt\)・・・③
\(z=z_0+ct\)・・・④

となり、②③④を直線\(l\)の媒介変数表示といい、\(t\)を媒介変数とよびます。

さらに\(a,b,c\)のどれもが\(0\)でないとき、②③④より\(t\)を消去すると

\(\displaystyle\frac{x-x_0}{a}=\displaystyle\frac{y-y_0}{b}=\displaystyle\frac{z-z_0}{c}\) \((=t)\)

と表すこともできます。

・直線のベクトル方程式(2点を通る直線)

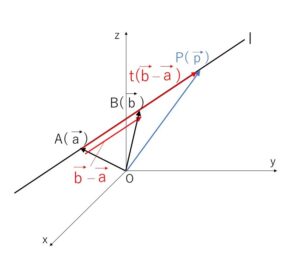
2点\(A(\vec{a}),B(\vec{b})\)を通る直線を\(l\)とすると

直線\(l\)は、「\(A(\vec{a})\) を通る 方向ベクトル\(\vec{b}-\vec{a}\) の直線」なので、直線上の点を\(P(\vec{p})\)とすると、直線\(l\)のベクトル方程式は

\(\vec{p}=\vec{a}+t(\vec{b}-\vec{a})\)・・・(i)
よって
\(\vec{p}=(1-t)\vec{a}+t\vec{b}\)・・・(ii)

ここで(ii)の右辺の係数の和が\(1\)になることに着目して、\(1-t=s\) とおくと次のように表すこともできます。

\(\vec{p}=s\vec{a}+t\vec{b}\),　\(s+t=1\)・・・(iii)

また \(A(a_1,a_2,a_3)\), \(B(b_1,b_2,b_3)\), \(P(x,y,z)\) とおいて原点\(O\)を基準とする位置ベクトルを考えると、(i)より

\((x,y,z)=(a_1,a_2,a_3)+t(b_1-a_1,b_2-a_2,b_3-a_3)\)

成分を比較して
\(x=a_1+t(b_1-a_1)\)・・・(iv)
\(y=a_2+t(b_2-a_2)\)・・・(v)
\(z=a_3+t(b_3-a_3)\)・・・(vi)

\(a_1≠b_1\), \(a_2≠b_2\), \(a_3≠b_3\) のとき、(iv)(v)(vi)から\(t\)を消去して

\(\displaystyle\frac{x-a_1}{b_1-a_1}=\displaystyle\frac{y-a_2}{b_2-a_2}=\displaystyle\frac{z-a_3}{b_3-a_3}\) \((=t)\)

次回以降、空間の直線に関する例題ついて扱っていきます。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線と直線の交点　back→同一平面上にある条件②