群数列について見ていきます。
・群数列
数列
\(1,1,3,1,3,5,1,3,5,7,1,3,5,7,9,1,\cdots\)
は次のように区切りを入れることで規則性を見つけることができます。
\(1|1,3|1,3,5|1,3,5,7|1,3,5,7,9|1,\cdots\)
このように数列をいくつかの組に分けたときこの組を群といい、群によって分けられた数列を群数列といいます。区切りで分けられた群について左から順に、第\(1\)群、第\(2\)群、・・・とよび、もとの数列の項の順番と、各群の項の順番について整理すると次の通りになります。

よってこの数列は群で分けることによって、各群では等差数列になっていることや、第\(k\)群の項数が\(k\)であることなどが分かり、特徴づけることができます。
(例題1)
分数を次のように並べた数列を考える。
\(\displaystyle\frac{1}{2},\displaystyle\frac{2}{3},\displaystyle\frac{1}{3},\displaystyle\frac{3}{4},\displaystyle\frac{2}{4},\displaystyle\frac{1}{4},\displaystyle\frac{4}{5},\displaystyle\frac{3}{5},\displaystyle\frac{2}{5},\displaystyle\frac{1}{5},\displaystyle\frac{5}{6},\cdots\)
(1)\(\displaystyle\frac{18}{25}\)は初めから数えて何項目にあるか。
(2)初めから数えて第\(666\)項目にある分数は何か。
(3)初項から第\(666\)項目までの和を求めよ。
\(\displaystyle\frac{1}{2}|\displaystyle\frac{2}{3},\displaystyle\frac{1}{3}|\displaystyle\frac{3}{4},\displaystyle\frac{2}{4},\displaystyle\frac{1}{4}|\displaystyle\frac{4}{5},\displaystyle\frac{3}{5},\displaystyle\frac{2}{5},\displaystyle\frac{1}{5}|\displaystyle\frac{5}{6},\cdots\)
すると、
(i)第\(k\)群の分母は1つ大きい\(k+1\)
(ii)第\(k\)群の分子は、\(k\)スタートで、\(1\)ずつ減っていく
(iii)第\(k\)群の項数は\(k\)
という特徴になっています。
(具体的に例えば第3群のときなどで考えて一般化するとよいです)
(解答)
(1)
\(\displaystyle\frac{1}{2}|\displaystyle\frac{2}{3},\displaystyle\frac{1}{3}|\displaystyle\frac{3}{4},\displaystyle\frac{2}{4},\displaystyle\frac{1}{4}|\displaystyle\frac{4}{5},\displaystyle\frac{3}{5},\displaystyle\frac{2}{5},\displaystyle\frac{1}{5}|\displaystyle\frac{5}{6},\cdots\)
と群で分けると、\(\displaystyle\frac{18}{25}\)は第\(24\)群にあり、第\(24\)群の初項は\(\displaystyle\frac{24}{25}\) であることから、\(\displaystyle\frac{18}{25}\)は、第\(24\)群の第\(7\)項(\(24-18+1\))である。
第\(k\)群の項数は\(k\)だから、第\(23\)群の最後の項はもとの数列で初めから数えて
\(1+2+3+\cdots+23=\displaystyle\frac{1}{2}\cdot23\cdot24\)
\(=276\) 項目である。
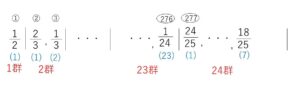
したがって \(276+7=283\) より、\(283\)項目。
(2)
第\(k\)群の最後の項は、もとの数列で初めから数えて
\(1+2+\cdots+k=\displaystyle\frac{1}{2}k(k+1)\) 項目。
よって、\(\displaystyle\frac{1}{2}k(k+1)≧666\) より
\(\displaystyle\frac{1}{2}k(k+1)≧666>\displaystyle\frac{1}{2}(k-1)k\)
として両側で挟んでもよいです。今回は上側だけ抑えて、最小値を考える方針でいきます。
\(k(k+1)≧1332\)・・・①
\(36\cdot37=1332\) だから、①を満たす最小の\(k\)は \(k=36\) であり、このとき①の不等式で等号が成り立つので、第\(666\)項目は第\(36\)群の最後の項である。
したがって第\(666\)項目は\(\displaystyle\frac{1}{37}\)
(3)
(第\(k\)群について)
\(\cdots|\displaystyle\frac{k}{k+1},\displaystyle\frac{k-1}{k+1},\cdots,\displaystyle\frac{1}{k+1}|\cdots\)
第\(k\)群のすべての項の和は
\(\displaystyle\frac{1}{k+1}\{k+(k-1)+\cdots+2+1\}\)
\(=\displaystyle\frac{1}{k+1}\cdot\displaystyle\frac{1}{2}k(k+1)\)
\(=\displaystyle\frac{1}{2}k\)
(2)より第\(36\)群の最後の項までの和を求めればよく、その和は
\(\displaystyle\sum_{k=1}^{36}\displaystyle\frac{1}{2}k\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{2}\cdot36\cdot37\)
\(=333\)
(例題2)
数列
\(1,1,3,1,3,5,1,3,5,7,1,3,5,7,9,1,\cdots\)
について
(1)\((k+1)\)回目に現れる\(1\)は第何項か。
(2)\(m\)回目に現れる\(17\)は第何項か。
(3)初項から\((k+1)\)回目の\(1\)までの項の和を求めよ。
(4)初項から第\(n\)項までの和を\(S_n\)とするとき、\(S_n>1300\) となる最小の\(n\)を求めよ。
と群に分けます。すると次の規則性があることが分かります。
(i)第\(t\)群は自然数の奇数を順に並べたもの (等差数列)
(ii)第\(t\)群の項数は\(t\)
(具体的に第\(3\)群などで考えて、一般化するとよい)
(解答)
(1)
\(1|1,3|1,\cdots\cdots|1,\cdots,(k群の最後)|1(←k+1回目),\cdots\)
\((k+1)\)回目の\(1\)は、\((k+1)\)群の初項だから
\((1+2+3+\cdots+k)+1\)
\(=\displaystyle\frac{1}{2}k(k+1)+1\)
\(=\displaystyle\frac{1}{2}k^2+\displaystyle\frac{1}{2}k+1\) より
第 \(\displaystyle\frac{1}{2}k^2+\displaystyle\frac{1}{2}k+1\) 項
(2)
\(2t-1=17\) から
\(t=9\)
よって、第\(9\)群に初めて\(17\)が現れる。
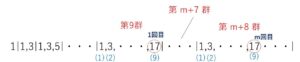
\(m\)回目に現れる\(17\)は、第 \(9+m-1=m+8\) 群の第\(9\)項なので
\(\{1+2+\cdots+(m+7)\}+9\)
\(=\displaystyle\frac{1}{2}(m+7)(m+8)+9\)
\(=\displaystyle\frac{1}{2}m^2+\displaystyle\frac{15}{2}m+37\)
よって
第 \(\displaystyle\frac{1}{2}m^2+\displaystyle\frac{15}{2}m+37\) 項
(3)
よって、「(\(k\)群の最後の項までの和)\(+1\)」です。\(k\)群の最後の項までの和については、まず群1つの和を計算して(文字を変えて\(t\)群として計算)、最後にシグマをとります。
(\(t\)群について)
\(\cdots|1,3,5,\cdots,2t-1|\cdots\)
\(t\)群の項の和は
\(1+3+5+\cdots+(2t-1)\)
\(=\displaystyle\frac{1}{2}t\{1+(2t-1)\}\)
\(=t^2\)
\(1|1,3|1,\cdots\cdots|1,\cdots,(k群の最後)|1(←k+1回目),\cdots\)
\((k+1)\)回目の\(1\)は \((k+1)\)群の初項だから、そこまでの和は 「第\(1~k\)群のすべての項の和\(+1\)」より
\(\displaystyle\sum_{t=1}^{k}t^2+1\)
\(=\displaystyle\frac{1}{6}k(k+1)(2k+1)+1\)
\(=\displaystyle\frac{1}{3}k^3+\displaystyle\frac{1}{2}k^2+\displaystyle\frac{1}{6}k+1\)
(4)
\(\displaystyle\frac{1}{6}k(k+1)(2k+1)\)
だから、この式から和が\(1300\)を超えるのは何群になるか調べます。3次不等式を直接解くのではなく、具体的に数値を色々代入していきます。
(3)より最初から第\(k\)群の最後の項までの和は、\(\displaystyle\frac{1}{6}k(k+1)(2k+1)\) だから
\(1300<\displaystyle\frac{1}{6}k(k+1)(2k+1)\) を満たす最小の\(k\)を求めると
\(\displaystyle\frac{1}{6}\cdot15\cdot16\cdot31=1240\)
\(\displaystyle\frac{1}{6}\cdot16\cdot17\cdot33=1496\)
より \(k=15\) が最小値で、第\(15\)群の最後の項までの和が\(1240\)
また、第\(16\)群の初項から第\(i\)項までの和は
\(1+3+\cdots+(2i-1)=i^2\) で ((3)の\(t\)群の和を参照)
\(7^2=49\), \(8^2=64\) だから
全体の初項から第\(16\)群の第\(7\)項までの和は\(1289\)
全体の初項から第\(16\)群の第\(8\)項までの和は\(1304\)
したがって、\(S_n\)が初めて\(1300\)より大きくなるのは 第\(16\)群の第\(8\)項まで和をとったときだから、そのときの\(n\)は
\(n=(1+2+\cdots+15)+8\)
\(=\displaystyle\frac{1}{2}\cdot15\cdot16+8\)
\(=128\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→群数列② back→奇数・偶数項と和