絶対値の和に関する例題です。
(例題1)
\(n\)が整数であるとき、
\(S=|n-1|+|n-2|+|n-3|+\cdots+|n-100|\)
の最小値を求めよ。また、そのときの\(n\)の値を求めよ。
なおこの(例題1)に関しては楽に解ける別解があります。
(解答)
(ア)\(n≦1\) (イ)\(n≧100\) (ウ)\(1<n<100\)
で場合分けします。(ア)(イ)は絶対値を一括して外すことができ、(ウ)は途中から絶対値を外すときに符号を変えることになります。
(ア)\(n≦1\)のとき
\(S=-(n-1)-(n-2)-(n-3)-\cdots-(n-100)\)
\(=-100n+(1+2+3+\cdots+100)\)
\(=-100n+\displaystyle\frac{1}{2}\cdot100\cdot101\)
\(=-100n+5050\)
これは単調減少であるから、\(n=1\) のとき 最小値 \(4950\) をとる。
(イ)\(n≧100\)のとき
\(S=(n-1)+(n-2)+(n-3)+\cdots+(n-100)\)
\(=100n-(1+2+3+\cdots+100)\)
\(=100n-5050\)
これは単調増加であるから、\(n=100\) のとき 最小値 \(4950\) をとる。
(ウ)\(1<n<100\)のとき
最初はしばらく絶対値の中身は正で、\(|30-30|=0\) を境目に、以降は \(|30-31|,|30-32|,\cdots\) と中身は負になります。

\(n\)は整数であるから
\(S=|n-1|+|n-2|+\cdots\)
\(+|n-(n-1)|+|n-n|+|n-(n+1)|+\cdots+|n-100|\)
\(=\{(n-1)+(n-2)+\cdots+1\}+\{1+2+\cdots+(100-n)\}\)
\(=\displaystyle\frac{1}{2}(n-1)n+\displaystyle\frac{1}{2}(100-n)(101-n)\)
\(=n^2-101n+5050\)
\(=(n-\displaystyle\frac{101}{2})^2+5050-\displaystyle\frac{101^2}{4}\)
よって \(\displaystyle\frac{101}{2}=50.5\) より
\(S\)は\(n=50,51\)で最小値をとりその値は
\(S=50^2-101\cdot50+5050\)\(=2500\)
以上から
最小値 \(2500\) (\(n=50,51\))
(別解)
\(S(n)=|n-1|+|n-2|+|n-3|+\cdots+|n-100|\)
とおくと
\(S(n+1)=|n|+|n-1|+|n-2|+\cdots+|n-99|\)
\(S(n+1)-S(n)\)
\(=|n|-|n-100|\)
(i)\(n<0\)のとき
\(|n|-|n-100|\)
\(=-n+(n-100)\)
\(=-100<0\)
よって
\(S(n)>S(n+1)\) (単調減少)
(ii)\(0≦n≦100\)のとき
\(|n|-|n-100|\)
\(=n+(n-100)\)
\(=2n-100\)
よって
(A)\(0≦n<50\) のとき
\(S(n)>S(n+1)\) (単調減少)
(B)\(n=50\) のとき
\(S(n)=S(n+1)\)
(C)\(50<n≦100\) のとき
\(S(n)<S(n+1)\) (単調増加)
(iii)\(n>100\) のとき
\(|n|-|n-100|\)
\(=n-(n-100)\)
\(=100>0\)
よって
\(S(n)<S(n+1)\) (単調増加)
以上から
\(\cdots>S(49)>S(50)=S(51)<S(52)<\cdots\)
となるから、\(n=50,51\) で\(S(n)\)は最小値をとりその値は
\(S(50)(=S(51))\)
\(=49+48+\cdots+1+0+1+2+\cdots+50\)
\(=2(1+2+\cdots+49)+50\)
\(=2\cdot\displaystyle\frac{1}{2}\cdot49\cdot50+50\)
\(=2500\)
(例題2)
\(x\)を実数とする。関数
\(f(x)=\displaystyle\sum_{k=1}^{100}|kx-1|\)
\(=|x-1|+|2x-1|+|3x-1|+\cdots+|100x-1|\)
を最小にする\(x\)の値を求めよ。
それぞれの絶対値は、\(x=1,\displaystyle\frac{1}{2},\displaystyle\frac{1}{3},\cdots,\displaystyle\frac{1}{100}\) が境目になっていますが、これを全部考えるわけにはいかないので、\(\displaystyle\frac{1}{m+1}≦x≦\displaystyle\frac{1}{m}\) (\(m=1,2,3,\cdots99\))と文字でおくことで処理していきます。
(ア)\(x≧1\) のとき
\(f(x)=|x-1|+|2x-1|+|3x-1|+\cdots+|100x-1|\)
\(=(x-1)+(2x-1)+(3x-1)+\cdots+(100x-1)\)
\(=(1+2+\cdots+100)x-100\)
\(=\displaystyle\frac{1}{2}\cdot100\cdot101x-100\)
\(=5050x-100\)
単調増加だから \(x=1\)で最小値をとる。
(イ)\(x≦\displaystyle\frac{1}{100}\) のとき
\(f(x)=|x-1|+|2x-1|+|3x-1|+\cdots+|100x-1|\)
\(=-(x-1)-(2x-1)-(3x-1)-\cdots-(100x-1)\)
\(=-5050x+100\)
単調減少だから \(x=\displaystyle\frac{1}{100}\)のとき最小値をとる。
(ア)(イ)より、\(\displaystyle\frac{1}{100}≦x≦1\) での最小値を考えればよい。
(ウ)\(\displaystyle\frac{1}{m+1}≦x≦\displaystyle\frac{1}{m}\) (\(m=1,2,3,\cdots99\)) のとき
\(m=30\) くらいを具体例にして一般化して下さい。
\(mx-1≦0\) かつ \((m+1)x-1≧0\) だから
\(x-1≦0\), \(2x-1≦0\), \(\cdots\), \(mx-1≦0\)
かつ
\((m+1)x-1≧0\), \((m+2)x-1≧0\), \(\cdots\), \(100x-1≧0\)
となるから
\(f(x)=|x-1|+|2x-1|+\cdots\)\(+|mx-1|+|(m+1)x-1|+\cdots+|100x-1|\)
\(=-\{(x-1)+(2x-1)+(mx-1)\}\)
\(+[\{(m+1)x-1\}+\{(m+2)x-1\}+\cdots+(100x-1)]\)
\(=\{-(1+2+\cdots+m)x+m\}\)
\(+[\{(m+1)+(m+2)+\cdots+100\}x-(100-m)]\)
\(=-\displaystyle\frac{1}{2}m(m+1)x+m+\displaystyle\frac{1}{2}(100-m)(101+m)x-100+m\)
\(=(-m^2-m+5050)x+(2m-100)\)・・・①
\(5050-m(m+1)\) とすると、\(m=70\) までは正で、\(m=71\)からは負になります。
ここで1次関数①の傾きは \(5050-m(m+1)\) だから
(i)\(1≦m≦70\) のとき正
(ii)\(71≦m≦99\) のとき負
であり
\(\displaystyle\frac{1}{m+1}≦x≦\displaystyle\frac{1}{m}\)
から求めます。例えば \(1≦m≦70\) のときは
\(\displaystyle\frac{1}{2}≦x≦1\), \(\displaystyle\frac{1}{3}≦x≦\displaystyle\frac{1}{2},\cdots\) \(,\displaystyle\frac{1}{71}≦x≦\displaystyle\frac{1}{70}\)
の合わせたもの \(\displaystyle\frac{1}{71}≦x≦1\) になります。
\(\displaystyle\frac{1}{m+1}≦x≦\displaystyle\frac{1}{m}\) だから
(i)\(\displaystyle\frac{1}{71}≦x≦1\) のときは傾きが正であることから\(f(x)\)は単調増加。
(ii)\(\displaystyle\frac{1}{100}≦x≦\displaystyle\frac{1}{71}\) のときは傾きが負であることから\(f(x)\)は単調減少。
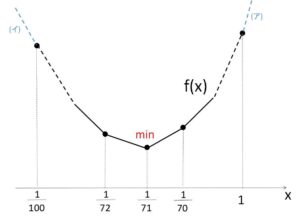
したがって
\(f(x)\)は \(x=\displaystyle\frac{1}{71}\) のとき最小値をとる。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→ガウス記号と数列 back→シグマとnCr