引き続き、確率・場合の数と漸化式に関する例題です。
今回は連立漸化式と破産の確率がテーマです。
(例題1)
1つのサイコロを\(n\)回振り、\(i\)回目に出た数を\(X_i\)とする。このとき、\(X_1^2+X_2^2+\cdots+X_n^{2}\) が\(3\)の倍数である確率を\(p_n\)、\(X_1^2+X_2^2+\cdots+X_n^{2}\) を\(3\)で割った余りが\(1\)である確率を\(q_n\)とする。
(1)\(p_n,q_n\)を\(p_{n-1},q_{n-1}\)を用いて表せ。
(2)\(a_n=p_n-\displaystyle\frac{1}{3}\), \(b_n=q_n-\displaystyle\frac{1}{3}\) とおくとき、\(a_n,b_n\) を \(a_{n-2},b_{n-2}\) (\(n≧2\)) を用いて表せ。
(3)\(p_{2n-1},q_{2n-1}\)を求めよ。
(解答)
(1)
今知りたいのは\(n-1\)と\(n\)のときの関係なので、\(X_1^1+X_2^2+\cdots+X_{n-1}^2\) に \(X_{n}^2\) を加えたときにどうなるかを考えます。\(X_1^1+X_2^2+\cdots+X_{n-1}^2\) を\(3\)で割った余りは\(0,1,2\)のどれかで、\(p_n\)については\(X_n^2\)を加えて\(3\)で割り切れるようになればよいので、組み合わせとしては、「余り\(0\)+余り\(0\)、余り\(2\)+余り\(1\)」の2パターンです。\(q_n\)についても同様に考えます。
\(1^2,2^2,3^2,4^2,5^2,6^2\)を3で割った余りは、順に\(1,1,0,1,1,0\)。
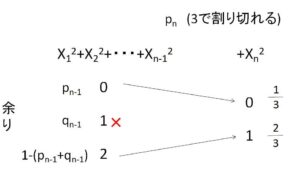
\(X_1^2+X_2^2+\cdots+X_n^{2}\) が\(3\)の倍数であるとき
(ア)\(X_1^2+X_2^2+\cdots+X_{n-1}^{2}\) と \(X_n^2\) のいずれも\(3\)の倍数
(イ)\(X_1^2+X_2^2+\cdots+X_{n-1}^{2}\)を\(3\)で割った余りが\(2\)、\(X_n^2\)を\(3\)で割った余りが\(1\)
のいずれかだから
\(p_{n}=p_{n-1}×\displaystyle\frac{1}{3}+(1-p_{n-1}-q_{n-1})×\displaystyle\frac{2}{3}\)
よって
\(p_{n}=-\displaystyle\frac{1}{3}p_{n-1}-\displaystyle\frac{2}{3}q_{n-1}+\displaystyle\frac{2}{3}\)
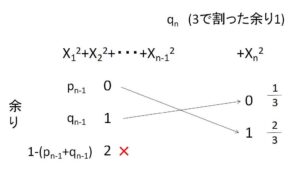
同様に、\(X_1^2+X_2^2+\cdots+X_n^{2}\) を\(3\)で割った余りが\(1\)のとき
(ウ)\(X_1^2+X_2^2+\cdots+X_{n-1}^{2}\)が\(3\)の倍数、\(X_n^2\)を\(3\)で割った余りが\(1\)
(エ)\(X_1^2+X_2^2+\cdots+X_{n-1}^{2}\)を\(3\)で割った余りが\(1\)、\(X_n^2\)が\(3\)の倍数
のいずれかだから
\(q_{n}=p_{n-1}×\displaystyle\frac{2}{3}+q_{n-1}×\displaystyle\frac{1}{3}\)
よって
\(q_{n}=\displaystyle\frac{2}{3}p_{n-1}+\displaystyle\frac{1}{3}q_{n-1}\)
(2)
\(p_{n}=-\displaystyle\frac{1}{3}p_{n-1}-\displaystyle\frac{2}{3}q_{n-1}+\displaystyle\frac{2}{3}\)
において、\(p_n=a_n+\displaystyle\frac{1}{3}\), \(q_n=b_n+\displaystyle\frac{1}{3}\) より
\(a_n+\displaystyle\frac{1}{3}=-\displaystyle\frac{1}{3}(a_{n-1}+\displaystyle\frac{1}{3})-\displaystyle\frac{2}{3}(b_{n-1}+\displaystyle\frac{1}{3})+\displaystyle\frac{2}{3}\)
整理して
\(a_n=-\displaystyle\frac{1}{3}a_{n-1}-\displaystyle\frac{2}{3}b_{n-1}\)・・・①
同様に
\(q_{n}=\displaystyle\frac{2}{3}p_{n-1}+\displaystyle\frac{1}{3}q_{n-1}\)
においては
\(b_n+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}(a_{n-1}+\displaystyle\frac{1}{3})+\displaystyle\frac{1}{3}(b_{n-1}+\displaystyle\frac{1}{3})\)
整理して
\(b_n=\displaystyle\frac{2}{3}a_{n-1}+\displaystyle\frac{1}{3}b_{n-1}\)・・・②
①②より
\(a_n=-\displaystyle\frac{1}{3}a_{n-1}-\displaystyle\frac{2}{3}b_{n-1}\)
(\(a_{n-1}\)は①の\(n\)を1つ下げたもの、\(b_{n-1}\)は②の下げたものを使って)
\(=-\displaystyle\frac{1}{3}(-\displaystyle\frac{1}{3}a_{n-2}-\displaystyle\frac{2}{3}b_{n-2})-\displaystyle\frac{2}{3}(\displaystyle\frac{2}{3}a_{n-2}+\displaystyle\frac{1}{3}b_{n-2})\)
\(=-\displaystyle\frac{1}{3}a_{n-2}\)
同様に①②より
\(b_n=\displaystyle\frac{2}{3}a_{n-1}+\displaystyle\frac{1}{3}b_{n-1}\)
\(=\displaystyle\frac{2}{3}(-\displaystyle\frac{1}{3}a_{n-2}-\displaystyle\frac{2}{3}b_{n-2})+\displaystyle\frac{1}{3}(\displaystyle\frac{2}{3}a_{n-2}+\displaystyle\frac{1}{3}b_{n-2})\)
\(=-\displaystyle\frac{1}{3}b_{n-2}\)
(3)
(2)より
\(a_k=-\displaystyle\frac{1}{3}a_{k-2}\)
\(k=2n-1\) のとき
\(a_{2n-1}=-\displaystyle\frac{1}{3}a_{2(n-1)-1}\) (1つずれた形)
(このまま解いてもよいですが、置き換えをすると)
\(a_{2n-1}=c_{n}\) とおくと
\(c_{n}=-\displaystyle\frac{1}{3}c_{n-1}\)
\(c_1=a_1=p_1-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}=0\)
よって
\(c_n=c_1\cdot(-\displaystyle\frac{1}{3})^{n-1}=0\)
ゆえに \(a_{2n-1}=0\) だから
\(p_{2n-1}=a_{2n-1}+\displaystyle\frac{1}{3}\)\(=\displaystyle\frac{1}{3}\)
同様に
\(b_k=-\displaystyle\frac{1}{3}b_{k-2}\)
\(k=2n-1\) のとき
\(b_{2n-1}=-\displaystyle\frac{1}{3}b_{2(n-1)-1}\)
\(b_{2n-1}=e_{n}\) とおくと
\(e_{n}=-\displaystyle\frac{1}{3}e_{n-1}\)
\(e_1=b_1=q_1-\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{3}\)
よって
\(e_n=e_1\cdot(-\displaystyle\frac{1}{3})^{n-1}=\displaystyle\frac{1}{3}(-\displaystyle\frac{1}{3})^{n-1}\)
ゆえに \(b_{2n-1}=\displaystyle\frac{1}{3}(-\displaystyle\frac{1}{3})^{n-1}\) だから
\(q_{2n-1}=b_{2n-1}+\displaystyle\frac{1}{3}\)\(=\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}(-\displaystyle\frac{1}{3})^{n-1}\)
(例題2)
「太郎君は\(2\)円、花子さんは\(3\)円持っている。」・・・(※)
いま、次のようなゲームをする。
じゃんけんをし、太郎君が勝ったならば花子さんから\(1\)円をもらえ、太郎君が負けたならば花子さんに\(1\)円を支払う。ただし、太郎君がじゃんけんに勝つ確率は\(\displaystyle\frac{2}{5}\)、負ける確率は\(\displaystyle\frac{3}{5}\)であり、どちらかの所持金が\(0\)となったときにその者が勝者となりゲームは終る。
このゲームで太郎君が勝つ確率を考えたい。
(1)\(A_n\) (\(0≦n≦5\)) を「太郎君の所持金が\(n\)円となった時からスタートし、花子さんの所持金が\(0\)円となる確率」とする。\(A_{n}\)を\(A_{n+1},A_{n-1}\) (ただし \(1≦n≦4\)とする) を用いて表せ。
(2) (1)の\(A_n\)において、\(A_1\)を求めよ。
(3)(※)の状態からスタートして、このゲームで太郎君が勝つ確率を求めよ。
(解答)
(1)
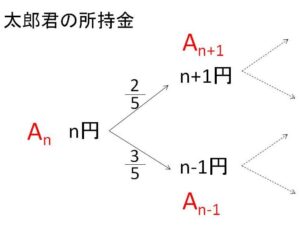
\(n\)円スタートで太郎君がゲームに勝つには
(ア)初回じゃんけんに勝って\(n+1\)円になり、ゲームに勝つ
(イ)初回じゃんけんに負けて\(n-1\)円になり、ゲームに勝つ
のいずれかであるから
\(A_n=\displaystyle\frac{2}{5}A_{n+1}+\displaystyle\frac{3}{5}A_{n-1}\) (\(1≦n≦4\))
(2)
\(A_0=0\), \(A_5=1\) である。
漸化式
\(A_{n+1}-\displaystyle\frac{5}{2}A_{n}+\displaystyle\frac{3}{2}A_{n-1}=0\) (\(A_{n+1}\)の係数を\(1\)にした)
より、特性方程式
\(x^2-\displaystyle\frac{5}{2}x+\displaystyle\frac{3}{2}=0\)
を解くと、\(x=1,\displaystyle\frac{3}{2}\) だから、漸化式は次のように変形できる。
\(A_{n+1}-A_{n}=\displaystyle\frac{3}{2}(A_{n}-A_{n-1})\)
\(A_{n+1}-\displaystyle\frac{3}{2}A_{n}=A_{n}-\displaystyle\frac{3}{2}A_{n-1}\)
(どちらも等比型)
よって
\(A_{n+1}-A_{n}=(A_1-A_0)(\displaystyle\frac{3}{2})^{n}=A_1(\displaystyle\frac{3}{2})^{n}\)・・・①
(\(n=0\)スタートなので\(n\)乗になる。具体的に\(n=0,1\)を代入して確かめるとよい)
\(A_{n+1}-\displaystyle\frac{3}{2}A_{n}=A_{1}-\displaystyle\frac{3}{2}A_{0}=A_1\)・・・②
(①-②)×2より
\(A_n=2A_1(\displaystyle\frac{3}{2})^{n}-2A_1\)・・・③ (不完全だが一般項)
\(n=5\)とすると
\(1=2A_1(\displaystyle\frac{3}{2})^{5}-2A_1\)
\(A_1\)について解くと
\(A_1=\displaystyle\frac{16}{211}\)
(3)
(2)の③より
\(A_n=2\cdot\displaystyle\frac{16}{211}(\displaystyle\frac{3}{2})^{n}-2\cdot\displaystyle\frac{16}{211}\) (完全な一般項)
求める確率は\(A_2\)だから
\(A_2=2\cdot\displaystyle\frac{16}{211}(\displaystyle\frac{3}{2})^{2}-2\cdot\displaystyle\frac{16}{211}\)
\(=\displaystyle\frac{72}{211}-\displaystyle\frac{32}{211}\)
\(=\displaystyle\frac{40}{211}\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→確率・場合の数と漸化式③ back→確率・場合の数と漸化式①