逆関数について見ていきます。
・逆関数
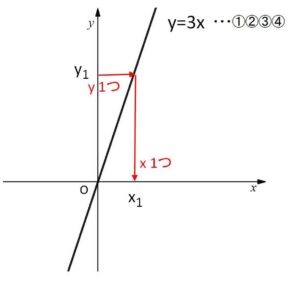
直線
\(y=3x\)・・・①
について\(y\)は\(x\)の関数となっているので
\(y=f(x)\ (=3x)\)・・・②
とおくことができますが、①を\(x\)について解くと
\(x=\displaystyle\frac{1}{3}y\)・・・③
と表すことができて、\(x\)についても\(y\)の関数になっています。よって
\(x=g(y)\ (=\displaystyle\frac{1}{3}y)\)・・・④
とおくことができます。このとき③と④について\(x,y\)を入れ替えると、
\(y=\displaystyle\frac{1}{3}x\)・・・(1)
\(y=g(x)\ (=\displaystyle\frac{1}{3}x)\)・・・(2)
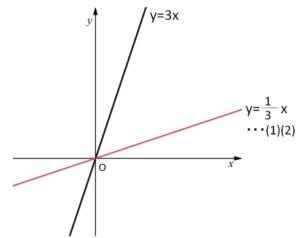
となり、この関数\(y=g(x)\)をもとの関数\(y=f(x)\)の逆関数とよび、\(g(x)\)を\(f^{-1}(x)\)で表します。もとの関数と逆関数のグラフを合わせたものは次の通りです。
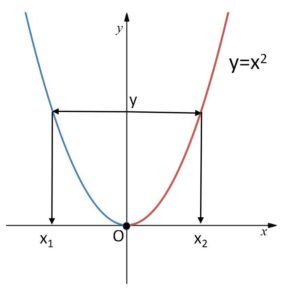
関数\(y=f(x)\)はいつでも逆関数をもつわけではなく、上の例のように「\(x\)についても\(y\)の関数になっている(\(y\)を1つ決めると\(x\)がただ1つ決まる)」・・・(※) ことが逆関数が存在する条件です。例えば \(y=f(x)=x^2\) は\(y=0\) 以外は正の値\(y\)について対応する\(x\)が2つ存在するので全体としては逆関数は存在しません。ただし、\(x=±\sqrt{y}\) とできるように、部分的に関数を分ける(この場合だと\(x\)の正負で分ける)ことで逆関数をもつようにすることができます。
\(y=f(x)=3x\)・・・①②
\(x=g(y)=\displaystyle\frac{1}{3}y\)・・・③④
はすべて同じ方程式です(③④は①②を式変形しただけなので)。よってグラフも全く同じものになります。しかし\(x,y\)を入れ替えた瞬間に方程式としては別のものになりグラフとしても別物になります(もとの関数との関連性はあります)。上の説明では先に③④の形にしてから\(x,y\)を入れ替えましたが、①②の形のまま入れ替えてもOKです。
また、関数\(g\)は\(f^{-1}\)とかくように定義したので、③④は
\(x=f^{-1}(y)\)
と表すことができます。したがって、「\(y=f(x)\) \(⇔\) \(x=f^{-1}(y)\)」 です(同じものを表す)。
また逆関数をもつ条件(※)については次のように表現されることもありますが、意味は同じです。
(ア)\(y=f(x)\)は単調増加関数、または 単調減少関数。
(イ)\(x_1≠x_2\) ならば \(f(x_1)≠f(x_2)\)
(イ)は\(x\)が違えば同じ\(y\)にはならない、つまり\(y\)1つについて\(x\)は1つのみ対応するということです。
・逆関数の性質
逆関数には以下のような性質があります。
(i)\(y=f(x)\) \(⇔\) \(x=f^{-1}(y)\) (同値)
(ii)\(y=f(x)\) と \(y=f^{-1}(x)\) では、定義域と値域が入れ替わる。
(iii)\(y=f(x)\) と \(y=f^{-1}(x)\) のグラフは、\(y=x\)について対称。
(解説)
(i)については前述の通り、(ii)については\(x,y\)を入れ替えたものが逆関数になるので明らかです。
(iii)については、座標平面上で 点\((x,y)\) と 点\((y,x)\) が直線 \(y=x\) について対称であることから分かります。
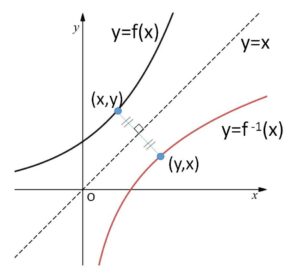
まず2点の対称性についてですが、
(ア)中点は\((\displaystyle\frac{x+y}{2},\displaystyle\frac{x+y}{2})\) で、\(y=x\) 上にある。
(イ)2点を通る直線の傾きが \(\displaystyle\frac{x-y}{y-x}=-1\) で、この直線は \(y=x\) と垂直
であることから対称。(\(x=y\)のときは2点が一致して、その点\((x,y)\)は\(y=x\)上にある)
そして、\(y=f(x)\)・・・①のグラフは①を満たす\((x,y)\)を座標とする点の集合なので、①で\(x,y\)を入れ替えてできた \(y=f^{-1}(x)\) のグラフは①のグラフと\(y=x\)について対称になります。
(例題)
関数 \(f(x)=ax+a^2\) について
(1)この関数が逆関数をもつ条件を求めよ。
(2)逆関数を求めよ。
(解答)
(1)
\(y=ax+a^2\)・・・① より
\(ax=y-a^2\)
ここで、\(a=0\) とすると
\(y=0\) (定数関数) となり、\(x\)は\(y\)の関数でないから逆関数は存在しない。
\(a≠0\) のときは
\(x=\displaystyle\frac{y}{a}-a\)・・・②
\(x\)は\(y\)の関数だから、逆関数は存在する。
したがって逆関数をもつ条件は \(a≠0\)
(2)
②の\(x,y\)を入れ替えると
\(y=\displaystyle\frac{x}{a}-a\)
また、もとの関数
\(y=ax+a^2\)・・・①
は1次関数で値域は実数全体。よって逆関数の定義域は実数全体だから
\(f^{-1}(x)=\displaystyle\frac{x}{a}-a\) (定義域は実数全体)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→逆関数の決定 back→円の方程式と無理関数