今回は、放物線が切り取る線分の長さについて考えていきます。切り取られる直線は\(x\)軸と一般的な直線 \(y=mx+n\) の場合がありますが、まずは簡単なほうの\(x\)軸から見ていきましょう。
・放物線が切り取る線分の長さ(\(x\)軸)
(問題1)
関数 \(y=2x^2-4x+k\) のグラフが\(x\)軸と交わる2点の間の距離が\(4\)であるように定数\(k\)の値を定めよ。
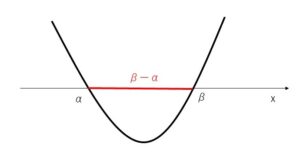
\(2x^2-4x+k=0\)の解を \(α,β\) (ただし\(α<β\))とすると、2点間の距離は \(β-α\) です。\(α,β\)を解の公式から\(k\)で表します。
(解答)
\(2x^2-4x+k=0\) を解くと
\(\displaystyle\frac{D}{4}=4-2k>0\)・・・① のとき
\(x=\displaystyle\frac{2±\sqrt{4-2k}}{2}\)
よって2点間の距離が\(4\)より
\(\displaystyle\frac{D}{4}=4-2k>0\)・・・① のとき
\(x=\displaystyle\frac{2±\sqrt{4-2k}}{2}\)
よって2点間の距離が\(4\)より
\(\displaystyle\frac{2+\sqrt{4-2k}}{2}-\displaystyle\frac{2-\sqrt{4-2k}}{2}=4\) から
\(\sqrt{4-2k}=4\) 両辺2乗して
\(4-2k=16\) より \(k=-6\)
これは①を満たす。
\(4-2k=16\) より \(k=-6\)
これは①を満たす。
※一般に \(y=ax^2+bx+c\) が\(x\)軸から切り取る線分の長さ\(L\)は、\(a>0\)のとき \(ax^2+bx+c=0\)の判別式を\(D\)とおくと、\(D>0\)のとき解の公式から、
\(L=\displaystyle\frac{-b+\sqrt{D}}{2a}-\displaystyle\frac{-b-\sqrt{D}}{2a}\)\(=\displaystyle\frac{\sqrt{D}}{a}\) となります。
\(L=\displaystyle\frac{-b+\sqrt{D}}{2a}-\displaystyle\frac{-b-\sqrt{D}}{2a}\)\(=\displaystyle\frac{\sqrt{D}}{a}\) となります。
(問題2)
放物線 \(y=x^2\)・・・① は 直線 \(y=x+k\)・・・② と異なる点\(A,B\)で交わり、\(A,B\)間の距離は\(\sqrt{10}\)である。定数\(k\)の値を求めよ。
放物線 \(y=x^2\)・・・① は 直線 \(y=x+k\)・・・② と異なる点\(A,B\)で交わり、\(A,B\)間の距離は\(\sqrt{10}\)である。定数\(k\)の値を求めよ。
今度は一般的な直線から切り取られる長さの問題です。線分が斜めを向いているので、交点を求めて三平方の定理を利用します。
(解答)
①、②から\(y\)を消去して
\(x^2-x-k=0\)・・・③
\(x^2-x-k=0\)・・・③
①と②が異なる2点で交わるとき③が2つの異なる実数解をもつときなので
\(D=1+4k>0\)・・・④
\(D=1+4k>0\)・・・④
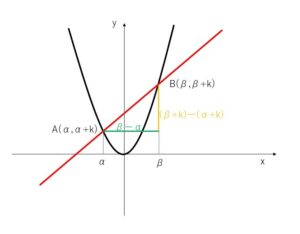
③の2解を\(α,β\) (ただし\(α<β\)) とおくと、\(α,β\)は①と②の交点の\(x\)座標となる。\(A,B\)は直線②上にあるので、\(A,B\)の座標は、\(A(α,α+k),B(β+β+k)\)となり、三平方の定理から
\(AB^2=(β-α)^2+\{(β+k)-(α+k)\}^2=2(β-α)^2\)・・・⑤
\(AB^2=(β-α)^2+\{(β+k)-(α+k)\}^2=2(β-α)^2\)・・・⑤
2次方程式③を解くと、
\(α=\displaystyle\frac{1-\sqrt{1+4k}}{2}\) \(β=\displaystyle\frac{1+\sqrt{1+4k}}{2}\) から
\(β-α=\sqrt{1+4k}\)
\(α=\displaystyle\frac{1-\sqrt{1+4k}}{2}\) \(β=\displaystyle\frac{1+\sqrt{1+4k}}{2}\) から
\(β-α=\sqrt{1+4k}\)
⑤と\(AB=\sqrt{10}\)より
\(10=2(1+4k)\) よって \(k=1\)
これは④を満たす。
\(10=2(1+4k)\) よって \(k=1\)
これは④を満たす。
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。