合成関数について見ていきます。
(※)
関数 \(y=f(x)\) の文字\(x,y\)は基本的にはどのような文字にしても問題ないので、関数を単純に\(f\)と記載することもあります。適宜利用してください。
・合成関数
関数 \(f(x)=x^2\), \(g(x)=2x+1\) があるとき、
\(y=f(x)\)・・・①
\(z=g(y)\)・・・②
とおいて、①を②に代入すると
\(z=g(f(x))=g(x^2)=2x^2+1\)
という新たな\(x\)の関数\(g(f(x))\)を作ることができます。
この例のように、2つの関数 \(y=f(x)\), \(z=g(y)\) があり、\(f(x)\)の値域\(y\)が\(g(y)\)の定義域に含まれるとき・・・(注1)、①を②に代入して得られる関数 \(z=g(f(x))\) を、\(f(x)\)と\(g(y)\) の合成関数とよびます。合成関数 \(g(f(x))\) は \((g \circ f)(x)\) ・・・(注2) と書かれることもあります。
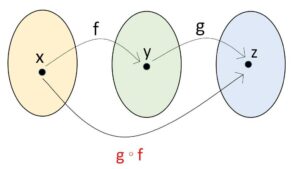
また、同様に3つ以上の関数についても合成関数を考えることができます。
(注1)
例えば、\(f(x)=x-3\)、\(g(x)=\sqrt{x}\)
のときの合成関数\(g(f(x))\)を形式的に考えると
\(g(f(x))=g(x-3)=\sqrt{x-3}\)
となり、根号の中身が負の値になる可能性がでてくるので合成関数を定義することができません。しかし、\(f(x)\)の値域を\(0\)以上に制限(\(g(x)\)の定義域に含まれるようにする)、つまり\(x≧3\)という制限をつけることで、合成関数を定義することができます。
(注2)
関数\(y=f(x)\)を、\(x\)に作用させて\(y\)という値に対応させる装置のようなものと捉えると、\(g \circ f(x)\) の作用の順は、\(f→g\) です。(左から読んで \(g→f\) の順に作用させない)
・合成関数の性質
合成関数について、結合法則は成り立ちますが、交換法則は成り立ちません。
結合法則
3つの関数、\(f(x),g(x),h(x)\) について
\((h \circ (g \circ f))(x)=((h \circ g) \circ f)(x)\)
意味は、\(g \circ f\)、\(h \circ g\) のどちらから先に合成関数を考えてもよいということです。
このことから、\((h \circ g \circ f)(x)\)と書くこともあります。
(証明)
\(s=f(x)\), \(t=g(s)\), \(u=h(t)\) とおく。
(左辺)について
\((g \circ f) (x)=g(f(x))=g(s)=t\) だから
\((h \circ (g \circ f))(x)=h(t)=u\)
(右辺)について
\(((h \circ g) \circ f)(x)=(h \circ g )(f(x))\)
\(=(h \circ g)(s)=h(g(s))=h(t)=u\)
交換法則
関数の大枠は最後に作用させる関数が決めるので、\(z=g(f(x))\) と \(z=f(g(x))\) は一般的には等しいとは限りません。つまり \((g \circ f )(x)=(f \circ g)(x)\) は一般的には成り立ちません。反例はいくらでもありますが、例えば
\(f(x)=x^2\), \(g(x)=2x+1\) だと
\(g(f(x))=g(x^2)=2x^2+1\)
\(f(g(x))=f(2x+1)=(2x+1)^2=4x^2+4x+1\)
・合成関数と逆関数
合成関数と逆関数について次の等式が成り立ちます。
関数\(f(x),g(x)\)が逆関数をもつとき
(i)\((f^{-1} \circ f)(x)=(f \circ f^{-1})(x)=x\)
(ii)\((g \circ f)^{-1}(x)=(f^{-1} \circ g^{-1})(x)\)
(解説)
(i)について
逆関数ともとの関数の合成関数\(l(x)\)は、\(l(x)=x\) (\(x\)に対して同じ値\(x\)を対応させるので恒等関数という) になります。交換法則が成り立つ特殊例の1つです。
(証明)
\(y=f(x)\) と \(x=f^{-1}(y)\) は同値だから
\((f^{-1} \circ f)(x)=f^{-1}(f(x))=f^{-1}(y)=x\)
同様に
\((f \circ f^{-1})(y)=f(f^{-1}(y))=f(x)=y\)
\(y\)を\(x\)に置きかえて
\((f \circ f^{-1})(x)=x\)
(ii)について
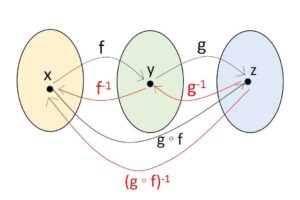
図より
\((g \circ f)^{-1}(z)=f^{-1}(g^{-1}(z))=(f^{-1} \circ g^{-1})(z)\)
変数を\(x\)にすれば
\((g \circ f)^{-1}(x)=(f^{-1} \circ g^{-1})(x)\)
演習は次回以降にします。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→合成関数に関する例題① back→合成関数ともとの関数のグラフの共有点(y=x 上にない点)