合成関数と方程式に関する例題です。
(例題1)
\(f(x)=x^2+2x+a\) について、\(x\)の方程式 \(f(x)=0\) が相異なる2つの実数解をもち、方程式 \(f(f(x))=0\) が重解\(γ\)をもつという。\(γ\)および\(a\)の値を求めよ。
(解答)
\(f(x)=x^2+2x+a\) において
\(x^2+2x+a=0\) の相異なる2つの実数解を\(α,β\) (\(α≠β\)) とすると、
\(αβ=a\) より\(a\)は実数。
判別式
\(\displaystyle\frac{D}{4}=1-a>0\) より
\(a<1\)
解と係数の関係から
\(α+β=-2\)・・・①
\(αβ=a\)・・・②
また \(f(x)=(x-α)(x-β)\) より
\(f(f(x))=(f(x)-α)(f(x)-β)\)
(ア)一方が重解をもつ (イ)それぞれ1つずつ共通解をもつ
場合があります。しかし(イ)は\(α≠β\)より不適です。
ここで、\(y=f(x)\)のグラフと、\(y=α\), \(y=β\) のグラフの交点の\(x\)座標を考えると、
\(f(x)-α=0\) と \(f(x)-β=0\) に共通解がないことが分かる。
よって\(α,β\)の対称性から
\(f(x)-α=0\)
つまり
\(x^2+2x+a-α=0\)
が重解\(γ\)をもつとしてよい。
ゆえに
\(γ\)\(=-\displaystyle\frac{2}{2}\)\(=-1\)
\(\displaystyle\frac{D}{4}=\)\(1-(a-α)=0\)・・・③
③より
\(α=a-1\)
これと①より
\(β=-a-1\)
よって②より
\((a-1)(-a-1)=a\)
\(a^2+a-1=0\)
\(a=\displaystyle\frac{-1±\sqrt{5}}{2}\) (\(a<1\)を満たす)
(例題2)
\(x\)に関する方程式
\((x^2-2x+a)^2+(x^2-2x+a)+b=0\)
(\(a,b\)は実数の定数)
の実数解はちょうど2個であり、\(0<x<1\) の範囲にはただ1つの解しかないという。ただし、\(b<\displaystyle\frac{1}{4}\) とする。このとき、点\((a,b)\)の存在する範囲を図示せよ。
(解答)
\((x^2-2x+a)^2+(x^2-2x+a)+b=0\)・・・①において
\(x^2-2x+a=X\)・・・② とおくと、①は
\(X^2+X+b=0\)・・・③
③の判別式は
\(D=1-4b>0\) (∵\(b<\displaystyle\frac{1}{4}\))
となるから、③は異なる2つの実数解をもつ。
\(x^2-2x+a=α\), \(x^2-2x+a=β\)
の解になります。問題の設定からこの2つの方程式のうち、「片方が実数解をもたず、片方が実数解を2つもち かつ その一方が\(0<x<1\)の範囲にある」ということになります。
解の配置なのでグラフを考えていきますが、③②の左辺のグラフ
\(f(X)=X^2+X+b\), \(g(x)=x^2-2x+a\)
において、\(x^2-2x+a=X\)・・・② から \(Y=f(X)\)の\(X\)座標が\(y=g(x)\)の\(y\)座標に対応していることに注意します。
以下グラフを参照しながら読んでください。\(y=g(x)\) のグラフは軸が\(x=1\)で固定で、\(g(0)=a\), \(g(1)=a-1\)。よって、\(f(X)=0\) の1つの実数解は \(a-1<X<a\) の範囲にあればよく、もう1つが \(X<a-1\) の範囲にあればよいことになります。
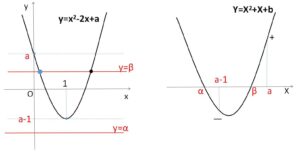
\(X^2+X+b=0\) の2つの異なる実数解を\(α,β\) (\(α<β\)) とし
\(g(x)=x^2-2x+a\)
\(f(X)=X^2+X+b\)
とおく。\(X,x\)の関係式 \(x^2-2x+a=X\)・・・② より
\(x^2-2x+a=α\)
\(x^2-2x+a=β\)
の実数解がもとの方程式①の実数解になるので、問題文の条件から、\(y=g(x)\) と \(y=α\) のグラフが共有点をもたず、\(y=g(x)\) と \(y=β\) のグラフが異なる2つの共有点をもち、かつ\(0<x<1\)の範囲で1つだけ共有点をもてばよいから、上左図より
\(α<a-1<β<a\)
よって右上図より求める条件は
\(f(a-1)<0\) かつ \(f(a)>0\)
\((a-1)^2+(a-1)+b<0\)
かつ
\(a^2+a+b>0\)
ゆえに
\(-a^2-a<b<-a^2+a\)・・・④
\(b<\displaystyle\frac{1}{4}\) も合わせて④を図示すると次の通り。
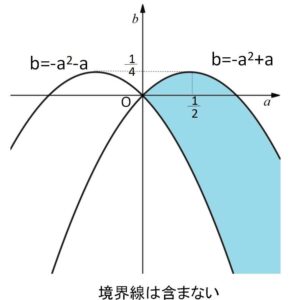
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→合成関数に関する例題②(分数関数・2次関数)