関数(三角関数)の極限を利用する図形問題です。
(例題1)
1直線上に3点\(O,A,B\)をこの順序にとり、\(OA=1\)、\(AB=2\) となるようにする。\(O\)を通り\(OA\)に垂直な直線上の動点を\(P\)とし、\(OP=h\)、\(\angle OPA=α\)、\(\angle APB=β\) とするとき、\(\displaystyle\lim_{h \to \infty}\displaystyle\frac{α}{β}\) を求めよ。
(解答)
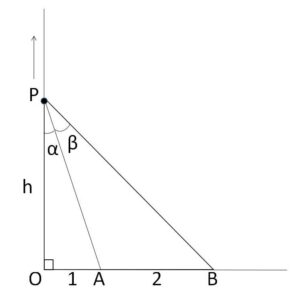
図より
\(\tanα=\displaystyle\frac{1}{h}\)・・・①
\(\tan(α+β)=\displaystyle\frac{3}{h}\)
加法定理より
\(\displaystyle\frac{\tanα+\tanβ}{1-\tanα\tanβ}=\displaystyle\frac{3}{h}\)
(\(\tanβ\)について解いていく)
\({\tanα+\tanβ}=\displaystyle\frac{3}{h}(1-\tanα\tanβ)\)
\((1+\displaystyle\frac{3}{h}\tanα)\tanβ=\displaystyle\frac{3}{h}-\tanα\)
①を代入して
\((1+\displaystyle\frac{3}{h^2})\tanβ=\displaystyle\frac{2}{h}\)
よって
\(\tanβ\)\(=\displaystyle\frac{\displaystyle\frac{2}{h}}{1+\displaystyle\frac{3}{h^2}}\)\(=\displaystyle\frac{2h}{h^2+3}\)・・・②
①②からも \(\tanα,\tanβ→0\) になることは分かりますが、\(\tanθ=0\) のとき、\(θ=kπ\) (\(k\)は整数) の可能性があるので、やはり図も使って判断する必要があります。
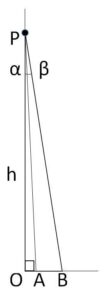
図より \(h \to \infty\) のとき、\(α \to +0\)、\(β \to +0\) であり
\(\displaystyle\frac{α}{β}=\displaystyle\frac{α}{\tanα}\cdot\displaystyle\frac{\tanβ}{β}\cdot\displaystyle\frac{\tanα}{\tanβ}\)
\(=\displaystyle\frac{α}{\tanα}\cdot\displaystyle\frac{\tanβ}{β}\cdot\displaystyle\frac{h^2+3}{2h^2}\) (①②より)
\(=\displaystyle\frac{α}{\tanα}\cdot\displaystyle\frac{\tanβ}{β}\cdot\displaystyle\frac{1+\displaystyle\frac{3}{h^2}}{2}\)
よって
\(\displaystyle\lim_{h \to \infty}\displaystyle\frac{α}{β}=\displaystyle\frac{1}{2}\)
(例題2)
平面上に半径\(1\)の円\(C\)がある。この円に外接し、さらに隣り合う2つが互いに外接するように、同じ大きさの\(n\)個の円を図(例1)のように配置し、その一つの円の半径を\(R_n\)とする。また、円\(C\)に内接し、さらに隣り合う2つが互いに外接するように、同じ大きさの\(n\)個の円を図(例2)のように配置し、その一つの円の半径を\(r_n\)とする。ただし、\(n≧3\) とする。
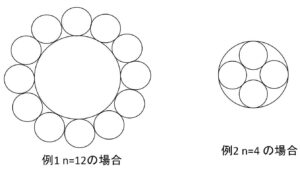
(1)\(R_n,r_n\) を求めよ。
(2)\(\displaystyle\lim_{n \to \infty}n^2(R_n-r_n)\) を求めよ。
(解答)
円\(C\)と隣り合う2つの円(合計3つ)を取り出して、図形的に半径を求めます。
中心を結ぶと三角形ができるので、余弦定理などが思い浮かびますが2次式になるのでやや面倒です。そこで2等辺三角形であることに着目して、中線(垂線になる)をひくと楽に計算できます。
(解答)
まず\(R_n\)について
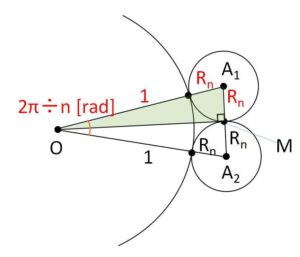
円\(C\)と隣り合う円2つを取り出して、中心を結ぶと二等辺三角形ができる。どの隣り合う2つの円を取り出しても同じ二等辺三角形ができるので、図の \(\angle A_1OA_2=\displaystyle\frac{2π}{n}\)
よって、\(A_1A_2\)の中点を\(M\)とすれば(ちょうど接点になる)、直角三角形\(OA_1M\)について
\((1+R_n)\sin(\displaystyle\frac{2π}{n}\cdot\displaystyle\frac{1}{2})=R_n\)
したがって
\(R_n(1-\sin\displaystyle\frac{π}{n})=\sin\displaystyle\frac{π}{n}\)
\(n≧3\)より \(1-\sin\displaystyle\frac{π}{n}≠0\) だから
\(R_n=\displaystyle\frac{\sin\displaystyle\frac{π}{n}}{1-\sin\displaystyle\frac{π}{n}}\)
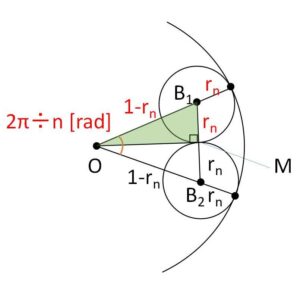
同様に\(r_n\)についても図より
\((1-r_n)\sin(\displaystyle\frac{2π}{n}\cdot\displaystyle\frac{1}{2})=r_n\)
したがって
\(r_n=\displaystyle\frac{\sin\displaystyle\frac{π}{n}}{1+\sin\displaystyle\frac{π}{n}}\)
(2)
\(\displaystyle\lim_{n \to \infty}n^2(R_n-r_n)\)
\(=\displaystyle\lim_{n \to \infty}n^2(\displaystyle\frac{\sin\displaystyle\frac{π}{n}}{1-\sin\displaystyle\frac{π}{n}}-\displaystyle\frac{\sin\displaystyle\frac{π}{n}}{1+\sin\displaystyle\frac{π}{n}})\)
\(=\displaystyle\lim_{n \to \infty}n^2\displaystyle\frac{2\sin^2\displaystyle\frac{π}{n}}{1-\sin^2\displaystyle\frac{π}{n}}\)
\(=\displaystyle\lim_{n \to \infty}2\cdot\displaystyle\frac{\left(\displaystyle\frac{\sin\displaystyle\frac{π}{n}}{\displaystyle\frac{π}{n}}\right)^2}{1-\sin^2\displaystyle\frac{π}{n}}\cdotπ^2\) (最後の\(π^2\)は調整用)
\(=2\cdot\displaystyle\frac{1^2}{1-0}\cdotπ^2\)
\(=2π^2\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→極限と条件式 back→三角関数の極限③