最大値・最小値の定理と、中間値の定理について見ていきます。
・最大値・最小値の定理
連続関数 \(f(x)=x^2+1\) は、閉区間 \(1≦x≦2\) において 「最小値\(f(1)=2\)、最大値\(f(2)=5\)」をとります。しかし、例えば \(1<x≦2\) においては、最大値\(f(2)=5\)をとりうりますが、最小値は存在しません。
一般に連続な関数\(f(x)\)について次のことが成り立ちます。
閉区間で連続な関数は、その閉区間で最大値および最大値をもつ。
(解説)
閉区間で連続な関数\(y=f(x)\)は、区間の両端で\(y\)の値が存在し、区間で\(y\)の値が途切れなく変化するので、そのうち\(y\)の値が最大なものが最大値、最小なものが最小値になるということです。
ポイントは連続と閉区間です。この一方でも欠けると定理は成り立ちません。閉区間(\(a≦x≦b\))でないといけないので、\(a<x<b\) (開区間)、\(a<x≦b\)、\(a≦x\)、などの区間ではダメです。(最大値・最小値の一方をもつことはある)
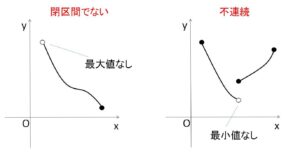
・中間値の定理
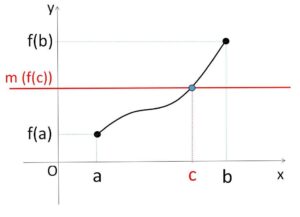
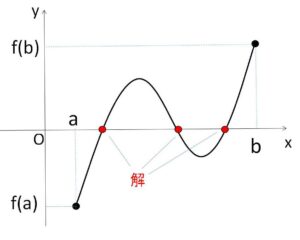
関数\(y=f(x)\)が閉区間\([a,b]\)において連続ならば、この区間で\(y=f(x)\)のグラフは切れ目がなく続いています。よって、\(f(x)\)は\(f(a)\)と\(f(b)\)の間のすべての値をとるので、次のことが成り立ちます。
関数\(f(x)\)が閉区間\([a,b]\)において連続で、\(f(a)≠f(b)\) ならば、\(f(a)\)と\(f(b)\)の間の任意の値\(m\)に対して
\(f(c)=m\)
となるような\(c\)が\(a\)と\(b\)の間に少なくとも1つ存在する。
(解説)
\(f(a)\)と\(f(b)\)の間の値(中間の値)\(m\)について、\(y=f(x)\)の グラフが \(y=m\) を横切り、それに対応する\(c\)が存在するということです。(上の図では端点で最大最小値をとっているが、とらなくても構わない)。この定理も「連続と閉区間」が条件になり、どちらかの一方でも欠けると成り立ちません。
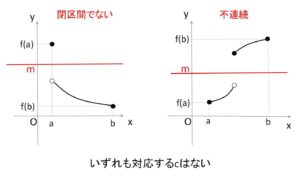
また、少なくとも1つ存在するということなので、2つ以上存在する場合もあります。そして、\(c\)の値は\(a,b\)の間にあるということしか分からず、具体的にどのような値になるかは別途調べる必要があります(具体的には求まらない場合もある)。\(c\)の存在だけが必要な証明問題などに有効です(特に後程説明する方程式の解の存在でよく使う)。
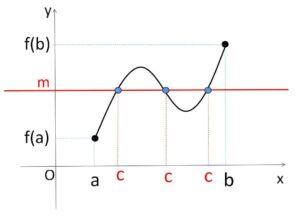
なお、「\(f(a)\)と\(f(b)\)の間、\(a\)と\(b\)の間」という表現は\(f(a),f(b),a,b\)を含まない解釈でよいです。含めても別に構わないのですが、例えば\(f(a)=m\)とすると、\(c=a\) として\(c\)が存在することが明らかなので、除いています。
また、\(f(a)=f(b)\) のときには間の値\(m\)がとれないので \(f(a)≠f(b)\) という条件がついています。
・中間値の定理(方程式の解の存在)
中間値の定理を利用することで、次の方程式の解の存在に関する定理が成り立つことが分かります。
関数\(f(x)\)が閉区間\([a,b]\)で連続で、\(f(a)\)と\(f(b)\)が異符号ならば
方程式 \(f(x)=0\)
は、\(a<x<b\) の範囲に少なくとも1つの実数解をもつ。
(解説)
\(f(a)\)と\(f(b)\)の符号が違うので、間の値として\(m=0\)がとれる。
よって中間値の定理から
\(f(c)=0\) (\(a<c<b\))
を満たす実数\(c\)が少なくとも1つ存在する。あとは\(c\)を\(x\)に変えればよい。
これも簡単にいうと、間の値 \(y=0\) つまり、\(x\)軸をグラフが最低1回は横切るということです。もちろん「閉区間で連続」という条件は必要です。
(例題1)
実数を係数とする3次方程式
\(x^3+a_1x^2+a_2x+a_3=0\)
は少なくとも1つの実数解をもつことを証明せよ。
(解答)
\(f(x)=x^3+a_1x^2+a_2x+a_3\) とおくと
\(x≠0\) のとき
\(f(x)=x^3(1+\displaystyle\frac{a_1}{x}+\displaystyle\frac{a_2}{x^2}+\displaystyle\frac{a_3}{x^3})\)
よって \(\displaystyle\lim_{x \to \infty}=\infty\)、\(\displaystyle\lim_{x \to -\infty}=-\infty\) となるから
十分大きな正の値\(b\)について、\(f(b)>0\)
十分小さな負の値\(a\)について、\(f(a)<0\)
したがって、\(f(x)\)は\([a,b]\)で連続だから、中間値の定理より 方程式 \(f(x)=0\) の実数解は少なくとも1つ存在する。
(例題2)
\(c\)は \(0<c<1\) を満たす定数とする。\(n\)を自然数とするとき、関数\(f_n(x)\)を
\(f_n(x)=-4x^3+3x^2+c^3(1-c^n)\)
と定める。\(0<x<1\)のとき、方程式 \(f_n(x)=0\) を満たす\(x\)がただ1つ存在することを示せ。
(解答)
\(f_n(x)=-4x^3+3x^2+c^3(1-c^n)\) において
\(f_n'(x)=-12x^2+6x=-6x(2x-1)\)
となるから、増減表は次の通り。
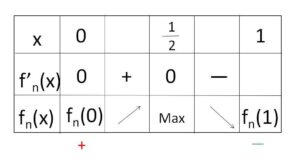
\(0<c<1\) より、\(0<c^3(1-c^n)<1\) となるから
\(f_n(0)=c^3(1-c^n)>0\)
\(f_n(1)=-1+c^3(1-c^n)<0\)
だから \(y=f_n(x)\) (\(0<x<1\)) のグラフは次の通り。
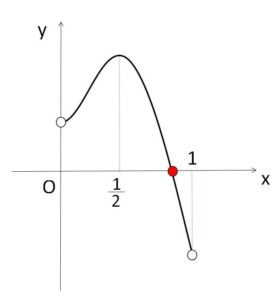
したがって、\(f_n(x)=0\) は \(0<x<1\) の範囲にただ1つの実数解をもつ。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→極限で表された関数