平均値の定理を利用する \(a_{n+1}=f(a_n)\) 型の漸化式の極限の例題です。
(例題)
\(f(x)=2^{\frac{x}{2}}\) とし、数列\(\{a_n\}\) を
\(a_1=1\)、\(a_{n+1}=f(a_n)\) (\(n=1,2,\cdots\))
によって定める。
(1)\(a_n<a_{n+1}\) (\(n=1,2,\cdots\)) を示せ。
(2)\(a_n<2\) (\(n=1,2,\cdots\)) を示せ。
(3)\(f(x)=x\) をみたす\(x\)を求めよ。
(4)\(f(α)=α\) のとき
\(α-a_{n+1}<\displaystyle\frac{α\log2}{2}(α-a_n)\) (\(n=1,2,\cdots\))
が成り立つことを示せ。
(5)\(\displaystyle\lim_{n \to \infty}a_n\) を求めよ。ただし \(e>2\) を用いてよい。
(解答)
(1)
\(a_n<a_{n+1}\) を数学的帰納法で示す。
(i)\(n=1\) のとき
\(a_1=1\)、\(a_2=2^{\frac{1}{2}}=\sqrt{2}\)
より、\(a_1<a_2\) だから成立。
(ii)\(n=k\) のとき (\(k=1,2,\cdots\))
\(a_k<a_{k+1}\) が成り立つと仮定する。
このとき、\(f(x)\)は増加関数だから
\(2^{\frac{a_k}{2}}<2^{\frac{a_{k+1}}{2}}\)
よって
\(a_{k+1}<a_{k+2}\) となるので、\(n=k+1\) のときも成立する。
(i)(ii)より、\(a_n<a_{n+1}\) (\(n=1,2,\cdots\)) が成り立つ。
(2)
\(a_n<2\) を数学的帰納法で示す。
(i)\(n=1\) のとき
\(a_1=1<2\) より成立。
(ii)\(n=k\) のとき (\(k=1,2,\cdots\))
\(a_k<2\) が成り立つと仮定する。
このとき
\(a_{k+1}=2^{\frac{a_k}{2}}<2^{\frac{2}{2}}=2\)
よって、\(a_{k+1}<2\) となり、\(n=k+1\) でも成立する。
(i)(ii)より、\(a_n<2\) (\(n=1,2,\cdots\)) が成り立つ。
(3)
しかしグラフを考え、適当に数値を代入すると、\(x=2,4\) が解になることは分かります。他に解があるかどうかについては、解答ではグラフの凸性に着目したいと思います。微分を利用してもOKです。
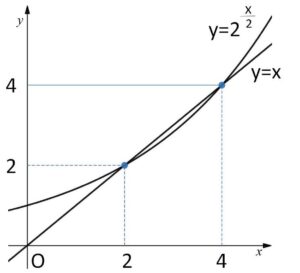
方程式 \(2^{\frac{x}{2}}=x\)
において、\(x=2,4\) を代入すると成り立つので、\(x=2,4\) は解である。
またグラフを考えると、\(y=2^{\frac{x}{2}}\) が下に凸であることから、直線\(y=x\)との交点の個数は3個以上にはならない。
よって \(f(x)=x\) を満たす\(x\)は
\(x=2,4\)
(4)
\(α-a_{n+1}<\displaystyle\frac{α\log2}{2}(α-a_n)\) は
\(f(α)-f(a_n)<\displaystyle\frac{α\log2}{2}(α-a_n)\)
と同じです。そしてこの不等式は平均値の定理と同じ形をしています。\(f(x)=2^{\frac{x}{2}}\) を微分すると、\(\log2\) が出てくることからも見当がつきます。
\(2^{\frac{α}{2}}=α\) (\(f(α)=α\))
(3),(2)より、\(α\)は\(2\)か\(4\)であることと、\(a_n<2\) より
\(a_n<2≦α\) だから
\(a_n<α\)
よって平均値の定理から
\(\displaystyle\frac{f(α)-f(a_n)}{α-a_n}=f'(c)\)・・・①
\(a_n<c<α\)・・・②
をみたす\(c\)が存在する。
\(f(x)=2^{\frac{x}{2}}\) より
\(f'(x)=\log2\cdot2^{\frac{x}{2}}\cdot\displaystyle\frac{1}{2}\)
ゆえに①より
\(α-a_{n+1}=2^{\frac{c}{2}}\cdot\displaystyle\frac{\log2}{2}(α-a_n)\)・・・③
ここで②より
\(2^{\frac{c}{2}}<2^{\frac{α}{2}}\ (=α)\) だから
\(\log2>0\)、\(α-a_n>0\) と③より
\(α-a_{n+1}<α\cdot\displaystyle\frac{\log2}{2}(α-a_n)\)
(5)
\(α=2,4\) のどちらを使うかは、\(a_n<2\) や 公比が\(1\)より小さくなるように \(α=2\) を選びます。後述しますが、グラフで階段状の動きを考えることでも 極限値が \(α=2\) であることは予想できます。
(4)で \(α=2\) とすると
\(2-a_{n+1}<\log2(2-a_n)\)
この不等式を繰り返し用いると
\(2-a_n<(\log2)^{n-1}(2-a_1)\)
\(a_n<2\) だから
\(0<2-a_n<(\log2)^{n-1}(2-a_1)\)・・・④
ここで \(e>2\) より \(0<\log 2<\log e=1\) だから
④において、はさみうちの原理から
\(\displaystyle\lim_{n \to \infty}(2-a_n)=0\)
したがって
\(\displaystyle\lim_{n \to \infty}a_n=2\)
(参考)
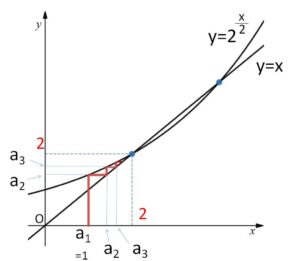
漸化式 \(a_{n+1}=f(a_n)\) (\(a_1=1\))
により \(a_1,a_2,a_3,\cdots\) を順に求める作業を、グラフ上の階段状の動きと対応させると、\(a_n\) が交点の1つの\(x(y)\)座標の \(2\) に近づくことが分かります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→グラフの増加率とガウス記号 back→平均値の定理と極限