曲線の凹凸(おうとつ)と、第2次導関数の関係について見ていきます。
・曲線の凹凸
2次関数 \(y=f(x)=x^2\)
のグラフは上左図のように下に膨らんでいる形をしています。この関数を微分すると、
\(f'(x)=2x\)
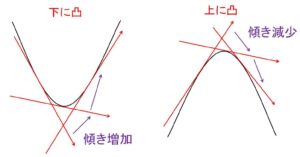
より、「\(x\)の値が増加するにつれて、\(f'(x)\)の値が増加」しています。つまり接線の傾きが\(x\)の値が増加するにつれて増加していることになりますが、これはグラフからも確認できます。
このように微分可能な関数\(f(x)\)について、ある区間で「\(x\)の値が増加するにつれて接線の傾きが増加する」とき、曲線 \(y=f(x)\) はその区間で下に凸(とつ)であるといいます。
同様に、ある区間で「\(x\)の値が増加するにつれて接線の傾きが減少する」ときは、曲線 \(y=f(x)\) はその区間で上に凸(とつ)であるといいます。
接線の傾き\(f'(x)\)の増減は、\(f'(x)\)が微分可能であるならば \(f”(x)\) の値の符号で決まるので、曲線の凹凸について次のことが成り立ちます。
関数 \(f(x)\) は2回微分可能であるとする。曲線 \(y=f(x)\) は、ある区間で
・\(f”(x)>0\) のとき、その区間で 下に凸
・\(f”(x)<0\) のとき、その区間で 上に凸
なお、\(f”(x)≧0\) (\(f”(x)≦0\)) の場合については、\(f”(x)=0\) となる\(x\)が点在しているに過ぎないときは、\(f'(x)\) は単調増加(単調減少)となるので、下に凸(上に凸)の曲線となります。
・変曲点
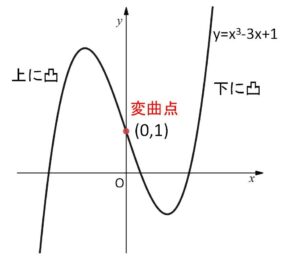
曲線 \(y=x^3-3x+1\)
の凹凸を調べてみると
\(y’=3x^2-3\)
\(y”=6x\)
より、\(x<0\) のとき上に凸、\(x>0\) のとき下に凸 となっています。よってこの曲線は、点\((0,1)\) を境目にして凹凸が変化しています。
このように、曲線 \(y=f(x)\) 上の 点\((a,f(a))\) を境目として、曲線の凹凸が変化するとき、この点を 曲線 \(y=f(x)\) の変曲点とよびます。
\(f(x)\)が2回微分可能であるとき、曲線の凹凸は第2次導関数の符号で決まるので、点\((a,f(a))\)について、\(x=a\) 前後で\(f”(x)\)の符号が変化するとき、この点は変曲点になります。
\(f”(x)\)が連続のとき、\(x=a\) が\(f”(x)\)の符号の変化の境目になっているので、\(f”(a)=0\) となります。
\(y=f(x)\)が2回微分可能で、\(f”(x)\)は連続であるとする。
点\((a,f(a))\) が変曲点ならば、\(f”(a)=0\)
(ただし逆は成り立たない)
よって変曲点を求める際には、第2次導関数の値が\(0\)になるものを探すことになりますが、それはあくまでも候補であることに注意してください。
\(f”(a)=0\) であっても、その前後で符号が変化しなければ変曲点にはなりません。
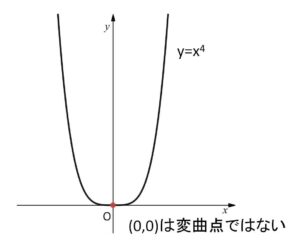
(例) \(f(x)=x^4\)
\(f”(x)=12x^2\) より、\(x=0\) のとき \(f”(x)=0\)。
しかし、\(x≠0\) で \(f”(x)>0\) となるので、点\((0,0)\) は変曲点ではない。
(\(y=x^4\) は実数全体の\(x\)で、下に凸)
凹凸や変曲点に関する演習は、グラフの概形のところでまとめて扱いたいと思います。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極値と第2次導関数 back→対数微分法と最大・最小値