円運動と単振動

等速円運動と単振動について見ていきます。

・等速円運動と単振動
点\(P\)が円周上を一定の速さで運動しているとき、この運動を等速円運動とよびます。

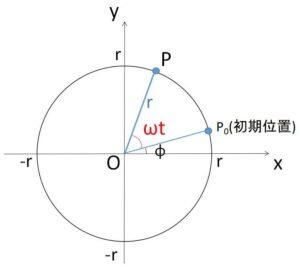
今、点\(P\)が、原点を中心とする半径\(r\ (>0)\)の円の周上を動く場合を考えます。

円弧は 「(半径)×{角(単位は\(\mathrm{rad}\))}」で表されるので、円周上を一定の速さで動くとき、動径\(OP\)を表す角は一定の割合\(ω\)で変化するので・・・(※)、時刻 \(t=0\) における角(初期値)を\(φ\)とすると、\(P(x,y)\)の座標は次のように表されることになります。

\(x=r\cos(ωt+φ)\)・・・①
\(y=r\sin(ωt+φ)\)・・・②

また、この\(ω\)を角速度とよびます。

ここで①②より、点\(P\)から\(x,y\)軸に下ろした垂線の足(点\(P\)の軸に落とした影)は、軸上を幅を\(r\)として往復運動することになり、この運動を単振動とよびます。

ところで①②より速度ベクトルと加速度ベクトルを求めると
\(\vec{v}=(-rω\sin(ωt+φ),rω\cos(ωt+φ))\)
\(=rω(-\sin(ωt+φ),\cos(ωt+φ))\)・・・③

\(\vec{α}=(-rω^2\cos(ωt+φ),-rω^2\sin(ωt+φ))\)
\(=rω^2(-\cos(ωt+φ),-\sin(ωt+φ))\)・・・④

となるので、速さと加速度の大きさはそれぞれ

\(|\vec{v}|=r|ω|\)　(速さは一定)
\(|\vec{α}|=rω^2\)

となります。

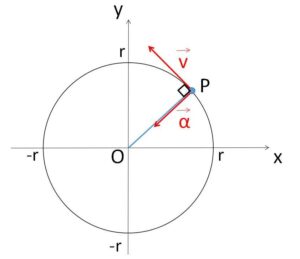
また、\(\overrightarrow{OP}=(\cos(ωt+φ),\sin(ωt+φ))\) と③④より
速度\(\vec{v}\)は\(\overrightarrow{OP}\)に垂直で、加速度\(\vec{α}\)は\(\overrightarrow{OP}\)とちょうど逆向きつまり円の中心に向かっていることになります。

(例題)
座標平面上で、点\(Q\)は点\(P\)を中心とする半径\(\displaystyle\frac{1}{3}\)の円周上を毎秒\(ω\)ラジアン (\(ω>0\)) の速さで正の向きに等速回転している。さらに点\(P\)は原点を中心とする半径\(1\)の円周上を毎秒\(1\)ラジアンの速さで正の向きに等速回転している。時刻 \(t=0\) において点\(P\)は\((1,0)\)、点\(Q\)は\((\displaystyle\frac{4}{3},0)\) にあるとして次の問いに答えよ。

問. ある時刻において点\(Q\)の加速度が零ベクトルになったとする。\(ω\)の値を求めよ。

(解答)

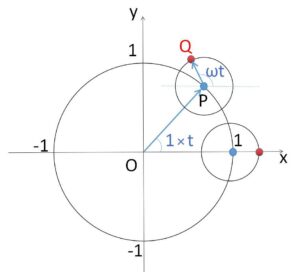
\(t\)秒後の点\(Q(x,y)\)の位置をベクトルで表すと、図より
\(\overrightarrow{OQ}=\overrightarrow{OP}+\overrightarrow{PQ}\)
\(=(\cos t,\sin t)+(\displaystyle\frac{1}{3}\cosωt,\displaystyle\frac{1}{3}\sinωt)\)

\(=(\cos t+\displaystyle\frac{1}{3}\cosωt,\ \sin t+\displaystyle\frac{1}{3}\sinωt)\)

よって点\(Q\)の速度ベクトル\(\vec{v}\)と加速度ベクトル\(\vec{α}\)は
\(\vec{v}=(-\sin t-\displaystyle\frac{ω}{3}\sinωt,\ \cos t+\displaystyle\frac{ω}{3}\cosωt)\)

\(\vec{α}=(-\cos t-\displaystyle\frac{ω^2}{3}\cosωt,\ -\sin t-\displaystyle\frac{ω^2}{3}\sinωt)\)

加速度ベクトルが\(\vec{0}\)になるとき
\(-\cos t-\displaystyle\frac{ω^2}{3}\cosωt=0\)
かつ
\(-\sin t-\displaystyle\frac{ω^2}{3}\sinωt=0\)

つまり
\(\cos t=-\displaystyle\frac{ω^2}{3}\cosωt\)・・・①
かつ
\(\sin t=-\displaystyle\frac{ω^2}{3}\sinωt\)・・・②

(\(\cos^2t+\sin^2t=1\) を利用して\(t\)を一気に消去します)

①\(^2\)+②\(^2\) より
\(1=\displaystyle\frac{ω^4}{9}\)

したがって
\(ω^4=9\)
\(ω^2=3\)
\(ω=\sqrt{3}\) \((>0)\)

(注)
十分性も確認しておくと①②より
\(\cos t=-\cos\sqrt{3}t\)・・・①
\(\sin t=-\sin\sqrt{3}t\)・・・②

よって
\(\cos t=\cos(\sqrt{3}t+π)\)・・・①’
\(\sin t=\sin(\sqrt{3}t+π)\)・・・②’

となるので
\(t=(\sqrt{3}t+π)+2nπ\)・・・③　(\(n\)は整数で、\(t≧0\) を満たすもの)
が①’②’を同時に満たす\(t\)の条件となり、確かに加速度が\(\vec{0}\)になる\(t\)は存在します。

実際③より
\(t=\displaystyle\frac{(2n+1)π}{1-\sqrt{3}}\)
が加速度が\(\vec{0}\)となる時刻です。(\(n\)は負の整数となる)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→グラフの上の点の速度・加速度　back→平面上の運動