2次不等式の文章問題を解いていきます。日本語で書かれた文章をうまく数式に翻訳します。
(問題)
直角をはさむ2辺の長さの和が\(24cm\)で、面積が\(54cm^2\)以上でかつ\(60cm^2\)以下である直角三角形を作りたい。2辺のうち短い方の長さをどのような範囲にすればよいか。
(解答)
短い方の辺の長さを\(x(cm)\)とすると、長い方は\(24-x(cm)\)
\(0<x<24-x\)より \(0<x<12\)・・・①
また、問題文の条件から
\(54≦\displaystyle\frac{1}{2}x(24-x)≦60\)
両辺に\(2\)を掛けて
\(108≦x(24-x)≦120\)となり、左辺と中辺、中辺と右辺に分けて整理すると
\(x^2-24x+108≦0\)・・・②
\(x^2-24x+120≧0\)・・・③
②を解くと、\((x-6)(x-18)≦0\) から
\(6≦x≦18\)・・・④
③を解くと \(x^2-24x+120=0\)の解は \(x=12±2\sqrt{6}\)より
\(x≦12-2\sqrt{6}\) または \(x≧12+2\sqrt{6}\)・・・⑤
ここで、\(\sqrt{6}=\sqrt{3}\sqrt{2}≒1.7×1.4≒2.4\) より
\(12-2\sqrt{6}≒7.2\) \(12+2\sqrt{6}≒16.8\) で
①④⑤を数直線上に図示すると以下のとおりとなる。
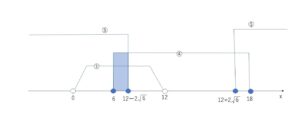
以上から求める短い方の長さの範囲は①かつ④かつ⑤より
\(6cm\) 以上 \(12-2\sqrt{6}cm\) 以下
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。