区分求積法について見ていきます。
・区分求積法
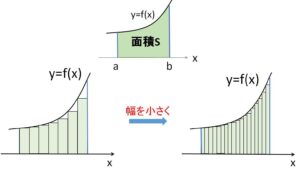
積分が発見されていない時代には、曲線で囲まれる面積を、簡単に計算できる長方形の短冊の面積の和として計算していました。
この方法だと実際の面積とのズレが生じてしまいますが、長方形の横の長さを限りなく短く、つまり分割する長方形の個数を限りなく大きくすると、長方形の面積の和は限りなく実際の面積に近づきます。よって次のことが成り立ちます。
「曲線で囲まれた面積」=「無限に分割された長方形の面積の和」 (無限級数)
以上のことをまとめると次のようになります。
関数 \(y=f(x)\) が 区間 \([a,b]\) で連続で、\(f(x)≧0\) とし、「\(x\)軸、\(y=f(x)\)、\(x=a\) と \(x=b\) で囲まれた図形」の面積を\(S\)とします。
\(S=\displaystyle\int_{a}^{b}f(x)dx\)
区間を\(n\)等分して、分点の\(x\)座標を小さい順に
\(x=x_1,x_2,\cdots,x_k,\cdots,x_{n-1}\)
とし、両端を \(a=x_0\)、\(b=x_n\)、横幅を \(Δx=\displaystyle\frac{b-a}{n}\) とします。
すると、\(x_k=a+kΔx\) (\(k=0,1,2,\cdots,n\)) となります。
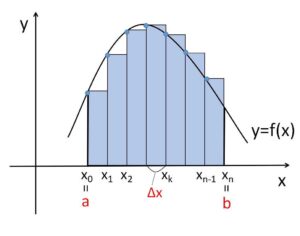
まず、長方形の左上端が \(y=f(x)\) 上にあるように考えると、\(n\)個の長方形の面積の和は
\(f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+\cdots+f(x_{n-1})Δx\)
\(=\displaystyle\sum_{k=0}^{n-1}f(x_k)Δx\)
となり、\(n \to \infty\) のとき、この長方形の面積の和は\(S\)に限りなく近づくので次の等式が成り立ちます。
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=0}^{n-1}f(x_k)Δx\)
(\(Δx=\displaystyle\frac{b-a}{n}\)、\(x_k=a+kΔx\))
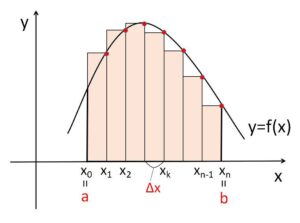
同様に、長方形の右上端が \(y=f(x)\) にあるように考えると、\(n\)個の長方形の面積の和は
\(f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+\cdots+f(x_{n})Δx\)
\(=\displaystyle\sum_{k=1}^{n}f(x_k)Δx\)
となり、\(n \to \infty\) のとき、この長方形の面積の和は\(S\)に限りなく近づくので次の等式が成り立ちます。
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}f(x_k)Δx\)
(\(Δx=\displaystyle\frac{b-a}{n}\)、\(x_k=a+kΔx\))
また、上記長方形の面積の求め方だと符号付きの面積となるので、定積分が符号付き面積を表すことを踏まえると \(f(x)<0\) の場合でも上記等式は成り立ちます。
そして、このように面積や体積を限りなく細かく分割して、和の極限として求める方法を区分求積法とよびます。区分求積法の考え方により、「定積分を和の極限に」、「和の極限を定積分」に変換することが可能です。どちらかというと部分和を求めることが困難な場合に、和の極限を定積分に変換して求めるという後者の使い方をすることが多いです。
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=0}^{n-1}f(x_k)Δx=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}f(x_k)Δx\)
(ただし \(Δx=\displaystyle\frac{b-a}{n}\)、\(x_k=a+kΔx\))
上記等式を、\(Δx\)と\(x_k\)を用いずに表すと次のようになります。
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\frac{b-a}{n}\displaystyle\sum_{k=0}^{n-1}f(a+k\cdot\displaystyle\frac{b-a}{n})=\displaystyle\lim_{n \to \infty}\displaystyle\frac{b-a}{n}\displaystyle\sum_{k=1}^{n}f(a+k\cdot\displaystyle\frac{b-a}{n})\)
よって特に \(a=0\)、\(b=1\) とすると
\(\displaystyle\int_{0}^{1}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{n-1}f(\displaystyle\frac{k}{n})=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}f(\displaystyle\frac{k}{n})\)
が成り立ち、この形式の区分求積法の等式もよく利用されます。
\(\displaystyle\int_{0}^{1}f(x)dx=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{n-1}f(\displaystyle\frac{k}{n})=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}f(\displaystyle\frac{k}{n})\)
(例)
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{π}{n}\left(\sin\displaystyle\frac{π}{n}+\sin\displaystyle\frac{2π}{n}+\cdots+\sin\displaystyle\frac{nπ}{n}\right)\)・・・(i)
(区分求積法2)を用いる場合、和の部分が \(f(\displaystyle\frac{k}{n})\) となるように
\(f(x)=\sinπx\) と選ぶことになります。よって(i)は
\(\displaystyle\lim_{n \to\infty}π\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\sinπ(\displaystyle\frac{k}{n})\)
\(=π\displaystyle\int_{0}^{1}\sinπxdx\)
\(=π\left[\displaystyle\frac{-\cosπx}{π}\right]_{0}^{1}\)
\(=2\)
一方(区分求積法1)を用いる場合は、横幅が\(\displaystyle\frac{π}{n}\) となるので、\(a=0\)、\(b=π\) とし、\(f(x)=\sin x\) と選ぶと(i)は
\(\displaystyle\lim_{n \to\infty}\displaystyle\frac{π-0}{n}\displaystyle\sum_{k=1}^{n}\sin(0+k\cdot\displaystyle\frac{π-0}{n})\)
\(=\displaystyle\int_{0}^{π}\sin xdx\)
\(=[-\cos x]_{0}^{π}\)
\(=2\)
余裕があればどちらも把握しておくとよいですが、(区分求積法2)のほうが分かりやすく、さらにこちらの方法だけで何とかなるのでこちらだけおさえておくとよいでしょう。
なお、長方形の短冊の和の個数が、\(\displaystyle\sum_{k=0}^{2n-1}\) のように変化する場合もありますが、この場合は適宜、定積分の上端下端を \(\displaystyle\int_{0}^{2}\) などのように変えて下さい。分からなくなったらグラフと長方形を描いて式と対応させて下さい。
また、\(\displaystyle\sum_{k=0}^{n}\) のように多少長方形の個数が増えても結論は変わりませんが、その場合は \(\displaystyle\sum_{k=0}^{n-1}\) とその他に分けて考えて下さい。
(例題)
次の極限を求めよ。
(1)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{\sqrt{n}}\left(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\right)\)
(2)\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{n+k}\)
(3)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{(n+1)^{α}+(n+2)^{α}+\cdots+(n+n)^{α}}{1^{α}+2^{α}+\cdots+n^{α}}\) (\(α>0\))
(解答)
(1)
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{\sqrt{n}}\left(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\right)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{\sqrt{n}}\cdot\displaystyle\frac{1}{\displaystyle\frac{\sqrt{n}}{\sqrt{n}}}\left(\displaystyle\frac{1}{\sqrt{1}}+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\right)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\left(\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{n}}}+\displaystyle\frac{1}{\sqrt{\displaystyle\frac{2}{n}}}+\displaystyle\frac{1}{\sqrt{\displaystyle\frac{3}{n}}}+\cdots+\displaystyle\frac{1}{\sqrt{\displaystyle\frac{n}{n}}}\right)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{\sqrt{\displaystyle\frac{k}{n}}}\)
\(=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{\sqrt{x}}dx\)
\(=[2\sqrt{x}]_{0}^{1}\)
\(=2\)
(2)
(同様に、\(\displaystyle\frac{k}{n}\) の形をつくります)
\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{n+k}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{\displaystyle\frac{n}{n}}\cdot\displaystyle\frac{1}{n+k}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}\)
\(=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx\)
\(=[\log|1+x|]_{0}^{1}\)
\(=\log2\)
(3)
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{(n+1)^{α}+(n+2)^{α}+\cdots+(n+n)^{α}}{1^{α}+2^{α}+\cdots+n^{α}}\)
(分母分子に、\(\displaystyle\frac{1}{n^α}\) を掛けて)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{(1+\displaystyle\frac{1}{n})^{α}+(n+\displaystyle\frac{2}{n})^{α}+\cdots+(n+\displaystyle\frac{n}{n})^{α}}{(\displaystyle\frac{1}{n})^{α}+(\displaystyle\frac{2}{n})^{α}+\cdots+(\displaystyle\frac{n}{n})^{α}}\)
(分母分子に \(\displaystyle\frac{1}{n}\) を掛けて)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}(1+\displaystyle\frac{k}{n})^α}{\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}(\displaystyle\frac{k}{n})^α}\)
(分母分子は収束し)
\(=\displaystyle\frac{\displaystyle\int_{0}^{1}(1+x)^αdx}{\displaystyle\int_{0}^{1}x^αdx}\)
\(=\displaystyle\frac{\left[\displaystyle\frac{(1+x)^{α+1}}{α+1}\right]_{0}^{1}}{\left[\displaystyle\frac{x^{α+1}}{α+1}\right]_{0}^{1}}\) (\(α>0\) より)
\(=\displaystyle\frac{2^{α+1}-1}{1}\)
\(=2^{α+1}-1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→区分求積法② back→微分の定義の利用と定積分