今回からは、2次方程式の解がある区間にある条件(解がある範囲内での値をとる条件)について考えていきます。まず最初に2解が正の値、負の値をとる条件から見ていきます。
・2次方程式の2解がともに正の値になる条件
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解をもち、その2解がともに正の値をとる条件について考えていきます。2解を2次関数のグラフとx\(軸\)の交点の\(x\)座標として考えるために、\(y=f(x)=ax^2+bx+c\) とおくと、条件を満たすグラフは次の通りです。
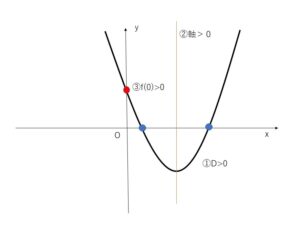
2解がともに正の値になる条件は
①まず2次方程式異なる2つの実数解をもつので、判別式 \(D>0\)
②つぎに、グラフの軸が\(y\)軸よりも右側にあるので、軸\(>0\)
③最後に\(f(0)\)の値が正なので、\(f(0)>0\)
まず①についてはよいですね。例えば判別式が負になったらそもそも実数解をもたないです。
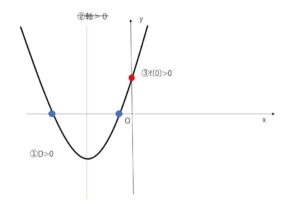
③について①②を満たしていても、\(f(0)≦0\)の場合\(f(x)\)は次のような位置になり\(0\)以下の解をもってしまいます。
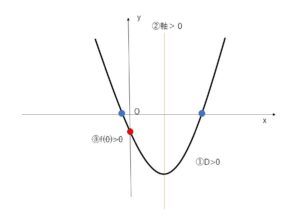
※条件①~③でグラフの位置を限定させる(位置を縛る)イメージです。
今度は2解が負になる条件です。2解が正の解の条件と考え方はほとんど一緒です。
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解をもち、その2解がともに負の値をとる条件について考えていきます。先ほどと同じく \(y=f(x)=ax^2+bx+c\) とおいて\(x\)軸との交点の位置関係を考えると、グラフは次の通りです。
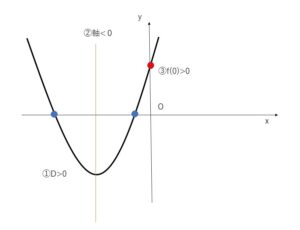
①まず2次方程式異なる2つの実数解をもつので、判別式 \(D>0\)
②つぎに、グラフの軸が\(y\)軸よりも左側にあるので、軸\(<0\)
③最後に\(f(0)\)の値が正なので、\(f(0)>0\)
・2解のうち1解が正の値、もう1解が負の値の場合
2次方程式 \(ax^2+bx+c=0\) (ただし\(a>0\))が2つの異なる実数解をもち、その2解のうち1つが正の値、もう1つが負の値をとる条件について考えていきます。
ふたたび、\(y=f(x)=ax^2+bx+c\) のグラフを考えると条件を満たすものは次の通り。
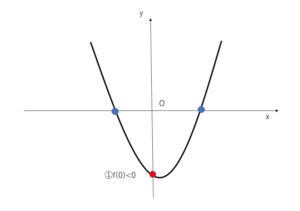
条件は
①\(f(0)<0\)
次に軸の条件がいらない理由ですが、軸が負の領域にあろうが、正の領域のあろうが\(f(0)<0\) という条件があるので、正と負の部分でグラフは\(x\)軸と交わることになります。(下図を参照してください)
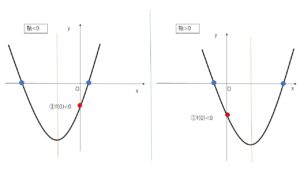
例題をやってみます。
(例題)
2次方程式 \(x^2-(m-10)x+m+14=0\) が次のような異なる2つの解をもつように、定数\(m\)の値の範囲を定めよ。
(1)ともに負 (2)正と負
(解答)
\(f(x)=x^2-(m-10)x+m+14\) とおく。
(1)\(y=f(x)\)が\(x\)軸の負の部分と異なる2点で交わるための条件を求める。
①判別式について \(D=(m-10)^2-4(m+14)>0\)
②軸について \(\displaystyle\frac{m-10}{2}<0\)
③\(f(0)=m+14>0\)
①より \(m^2-24m+44>0\) から \((m-2)(m-22)>0\)
よって \(m<2\), \(m>22\)・・・④
②より \(m<10\)・・・⑤
③より \(m>-14\)・・・⑥
④⑤⑥を満たす\(m\)の範囲は
\(-14<m<2\)
(2)
求める条件は、\(f(0)=m+14<0\)
よって \(m<-14\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。