ガウス記号と定積分

ガウス記号、整数部分と定積分の例題です。

(例題1)
実数\(x\)に対して、\(x\)を越えない最大の整数を\([x]\)で表す。\(n\)を正の整数とし
\(a_n=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{[\sqrt{2n^2-k^2}]}{n^2}\)
とおく。このとき、\(\displaystyle\lim_{n \to \infty}a_n\) を求めよ。

ガウス記号は不等式で評価することが基本になります。
\([x]≦x<[x]+1\) より、\(x-1<[x]≦x\) (ガウス記号が主役の式) です。\(x\)が整数だと、例えば \([3]=3\) となるので、片方には等号がつきます。
式の形から区分求積法をおそらく使うのでしょう。不等式ではさみこむおかけで、はさみうちの原理も使えます。

(解答)
\(\sqrt{2n^2-k^2}-1<[\sqrt{2n^2-k^2}]≦\sqrt{2n^2-k^2}\)
より
\(\displaystyle\frac{\sqrt{2n^2-k^2}}{n^2}-\displaystyle\frac{1}{n^2}<\displaystyle\frac{[\sqrt{2n^2-k^2}]}{n^2}≦\displaystyle\frac{\sqrt{2n^2-k^2}}{n^2}\)

\(k=1,2,\cdots,n\) まで変化させて辺々和をとると
\(\displaystyle\sum_{k=1}^{n}\left\{\displaystyle\frac{\sqrt{2n^2-k^2}}{n^2}-\displaystyle\frac{1}{n^2}\right\}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{[\sqrt{2n^2-k^2}]}{n^2}≦\displaystyle\sum_{k=1}^{n}\displaystyle\frac{\sqrt{2n^2-k^2}}{n^2}\)

(区分求積法が使えるように変形します)

\(\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{\sqrt{2n^2-k^2}}{n}-\displaystyle\frac{n}{n^2}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{[\sqrt{2n^2-k^2}]}{n^2}≦\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{\sqrt{2n^2-k^2}}{n}\)

よって
\(\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\sqrt{2-\left(\displaystyle\frac{k}{n}\right)^2}-\displaystyle\frac{1}{n}<a_n≦\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\sqrt{2-\left(\displaystyle\frac{k}{n}\right)^2}\)

\(n \to \infty\) のとき、両辺は
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\sqrt{2-\left(\displaystyle\frac{k}{n}\right)^2}=\displaystyle\int_{0}^{1}\sqrt{2-x^2}dx\)

(\(x=\sqrt{2}\sinθ\) で置換すると)

\(=\displaystyle\int_{0}^{\frac{π}{4}}\sqrt{2-2\sin^2θ}\ (\sqrt{2}\cosθdθ)\)

\(=\displaystyle\int_{0}^{\frac{π}{4}}2\cos^2θdθ\)

\(=\displaystyle\int_{0}^{\frac{π}{4}}(1+\cos2θ)dθ\)

\(=\left[θ+\displaystyle\frac{\sin2θ}{2}\right]_{0}^{\frac{π}{4}}\)

\(=\displaystyle\frac{π}{4}+\displaystyle\frac{1}{2}\)

に収束する。(円の面積の一部として計算してもよい)

したがってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}a_n=\displaystyle\frac{π}{4}+\displaystyle\frac{1}{2}\)

(例題2)
\(\displaystyle\sum_{n=1}^{40000}\displaystyle\frac{1}{\sqrt{n}}\) の整数部分を求めよ。

(解答)

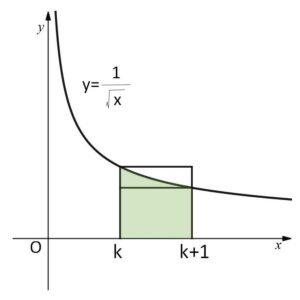
図より \(k=1,2,\cdots\) のとき
\(\displaystyle\frac{1}{\sqrt{k+1}}<\displaystyle\int_{k}^{k+1}\displaystyle\frac{1}{\sqrt{x}}dx<\displaystyle\frac{1}{\sqrt{k}}\)・・・①

(積分が両側にくるように変形します)
①の左側は、\(k \to k-1\) とすれば
\(\displaystyle\frac{1}{\sqrt{k}}<\displaystyle\int_{k-1}^{k}\displaystyle\frac{1}{\sqrt{x}}dx\)
となるので、①の右側と合わせて

\(\displaystyle\int_{k}^{k+1}\displaystyle\frac{1}{\sqrt{x}}dx<\displaystyle\frac{1}{\sqrt{k}}<\displaystyle\int_{k-1}^{k}\displaystyle\frac{1}{\sqrt{x}}dx\)・・・②

(積分が計算しやすいように、区間が\(1≦x≦40000\) になるように和をとります)

②の左側の不等式において、\(k=1,2,\cdots,39999\) として辺々加えると
\(\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx<\displaystyle\sum_{k=1}^{39999}\displaystyle\frac{1}{\sqrt{k}}\)
両辺に\(\displaystyle\frac{1}{\sqrt{40000}}\) を加えて(目標の式にする)

\(\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}\)・・・③

同様に②の右側の不等式で、\(k=2,3,\cdots,40000\) として辺々加えると
\(\displaystyle\sum_{k=2}^{40000}\displaystyle\frac{1}{\sqrt{k}}<\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx\)
両辺に\(\displaystyle\frac{1}{\sqrt{1}}\)を加えて

\(\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}<\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx+1\)・・・④

よって③④より
\(\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}<\displaystyle\int_{1}^{40000}\displaystyle\frac{1}{\sqrt{x}}dx+1\)

となるから
\([2\sqrt{x}]_{1}^{40000}+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}<[2\sqrt{x}]_{1}^{40000}+1\)

\(2(200-1)+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}<2(200-1)+1\)

\(398+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}\displaystyle\frac{1}{\sqrt{k}}<399\)

したがって整数部分は\(398\)である。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→漸化式と定積分と極限　back→定積分と極限