曲線で囲まれた面積は定積分で計算できます。
・定積分と面積
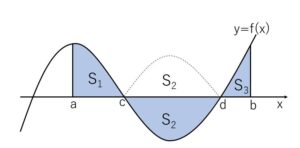
曲線 \(y=f(x)\) と \(x=a\)、\(x=b\) (\(a<b\)) で囲まれた面積\(S\ (=S_1+S_2+S_3)\)は次のように定積分で計算できます。
\(S=\displaystyle\int_{a}^{b}|f(x)|dx\)
証明など詳しくは →定積分と面積の関係 を参照して下さい。
定積分の結果は\(f(x)\)の符号が影響するので、\(f(x)<0\) の部分の定積分計算では負の値としてでてきます(符号付き面積となる)。したがって一般的には\(f(x)\)に絶対値をつけて定積分を計算することになりますが、実際に計算する際には負の部分と正の部分で場合分けすることになります。
よって上図では、\(S_1,S_2,S_3\)に分けて計算することになりますが、そのまま\(\displaystyle\int_{a}^{b}f(x)dx\) を計算した場合には、\(S_1-S_2+S_3\) の値がでてきてしまいます。
(例題)
次の曲線と直線で囲まれた部分の面積を求めよ。
(1)\(y=-\sin x\) (\(0≦x≦π\))、\(x\)軸
(2)\(y=\log(a^2-x^2)\)、\(x\)軸 (ただし \(a>1\))
(解答)
(1)
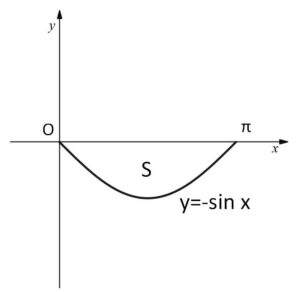
面積\(S\)は
\(S=-\displaystyle\int_{0}^{π}(-\sin x)dx=\displaystyle\int_{0}^{π}\sin xdx\)
\(=[-\cos x]_{0}^{π}\)
\(=2\)
(2)
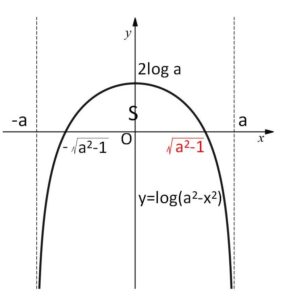
\(y=\log(a^2-x^2)\) の定義域は \(-a<x<a\)
また、グラフは\(y\)軸対称で、\(y\)切片は
\(y=\log(a^2-0)=2\log a>0\) (\(a>1\) より)
\(x≧0\) では単調減少であり、\(x\)軸との交点は
\(a^2-x^2=1\)
を解くと、\(x=±\sqrt{a^2-1}\)
したがって面積\(S\)は
\(S=2\displaystyle\int_{0}^{\sqrt{a^2-1}}\log(a^2-x^2)dx\)
(部分積分をして)
\(=2[x\log(a^2-x^2)]_{0}^{\sqrt{a^2-1}}-2\displaystyle\int_{0}^{\sqrt{a^2-1}}x\cdot\displaystyle\frac{-2x}{a^2-x^2}dx\)
\(=0-4\displaystyle\int_{0}^{\sqrt{a^2-1}}\displaystyle\frac{-x^2}{a^2-x^2}dx\)
(分子の次数が大きいので帯分数にして)
\(=-4\displaystyle\int_{0}^{\sqrt{a^2-1}}\left(1-\displaystyle\frac{a^2}{a^2-x^2}\right)dx\)
(部分分数分解する)
\(=-4\displaystyle\int_{0}^{\sqrt{a^2-1}}\left\{1-\displaystyle\frac{a^2}{(a-x)(a+x)}\right\}dx\)
\(=-4\displaystyle\int_{0}^{\sqrt{a^2-1}}\left\{1-\displaystyle\frac{a}{2}\left(\displaystyle\frac{1}{a-x}+\displaystyle\frac{1}{a+x}\right)\right\}dx\)
\(=-4\left[x-\displaystyle\frac{a}{2}\{-\log(a-x)+\log(a+x)\}\right]_{0}^{\sqrt{a^2-1}}\)
\(=-4\left[x-\displaystyle\frac{a}{2}\log\displaystyle\frac{a+x}{a-x}\right]_{0}^{\sqrt{a^2-1}}\)
\(=-4\sqrt{a^2-1}+2a\log\displaystyle\frac{a+\sqrt{a^2-1}}{a-\sqrt{a^2-1}}\)
\(=-4\sqrt{a^2-1}+2a\log(a+\sqrt{a^2-1})^2\)
\(=-4\sqrt{a^2-1}+4a\log(a+\sqrt{a^2-1})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2曲線で囲まれる面積①