引き続き2曲線で囲まれる面積の例題です。
(例題)
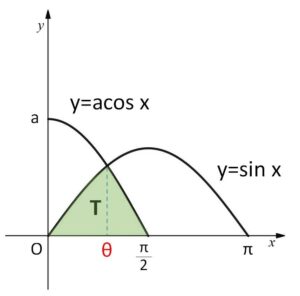
\(a\)を正の実数とする。座標平面において 曲線 \(y=\sin x\) (\(0≦x≦π\)) と\(x\)軸とで囲まれた図形の面積を\(S\)とし、曲線 \(y=\sin x\) (\(0≦x≦\displaystyle\frac{π}{2}\))、曲線 \(y=a\cos x\) (\(0≦x≦\displaystyle\frac{π}{2}\)) および\(x\)軸で囲まれた図形の面積を\(T\)とする。このとき \(S:T=3:1\) となるような\(a\)の値を求めよ。
次に\(T\)ですが、グラフの概形から2曲線が1点で交わることになり、この交点の\(x\)座標が積分計算で必要になってきます。\(\sin x=a\cos x\) を満たす\(x\)が交点の\(x\)座標ですが、これは具体的には分からないのでとりあえず文字\(θ\)でおくことにして、後で\(θ\)を消去する方針をとることにします。(\(\sinθ=a\cosθ\) が\(a,θ\)の関係式。\(a\)を消去して、\(\sinθ,\cosθ\)の値を求めてから\(a\)を決定する方針でもOKです)
(解答)
まず\(S\)について
\(S=\displaystyle\int_{0}^{π}\sin xdx=[-\cos x]_{0}^{π}\)
\(=2\)
次に\(T\)について
\(0≦x≦\displaystyle\frac{π}{2}\) の範囲では
\(y=a\cos x\) は単調減少、\(y=\sin x\) は単調増加で
\(a\cos0>\sin 0\)、\(a\cos\displaystyle\frac{π}{2}<\sin\displaystyle\frac{π}{2}\)
だから、2曲線はこの範囲でただ1つの交点をもつ。この交点の\(x\)座標を\(θ\)とおくと
\(a\cosθ=\sinθ\)・・・① (\(0<θ<\displaystyle\frac{π}{2}\))
よって
\(T=\displaystyle\int_{0}^{θ}\sin xdx+\displaystyle\int_{θ}^{\frac{π}{2}}a\cos xdx\)
\(=[-\cos x]_{0}^{θ}+a[\sin x]_{θ}^{\frac{π}{2}}\)
\(=-\cosθ+1+a(1-\sinθ)\)
ここで①より \(0<θ<\displaystyle\frac{π}{2}\) と \(a>0\) に注意すると
\(a=\tanθ\) だから
\(1+a^2=\displaystyle\frac{1}{\cos^2θ}\) より
\(\cosθ=\displaystyle\frac{1}{\sqrt{1+a^2}}\)
\(\sinθ=\sqrt{1-\cos^2θ}=\sqrt{\displaystyle\frac{a^2}{1+a^2}}\)
\(=\displaystyle\frac{a}{\sqrt{1+a^2}}\)
ゆえに
\(T=-\displaystyle\frac{1}{\sqrt{1+a^2}}+1+a(1-\displaystyle\frac{a}{\sqrt{1+a^2}})\)
\(=-\displaystyle\frac{1+a^2}{\sqrt{1+a^2}}+1+a\)
\(=-\sqrt{1+a^2}+1+a\)
\(T=\displaystyle\frac{1}{3}S\) だから
\(-\sqrt{1+a^2}+1+a=\displaystyle\frac{2}{3}\)
\(a+\displaystyle\frac{1}{3}=\sqrt{1+a^2}\)
両辺正の値だから2乗して
\(a^2+\displaystyle\frac{2}{3}a+\displaystyle\frac{1}{9}=a^2+1\)
したがって
\(a=\displaystyle\frac{4}{3}\) (\(a>0\)を満たす)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→y軸方向の積分と面積 back→2曲線で囲まれる面積①