トロコイドについてです。
・トロコイド
円をある曲線(または直線)\(C\)に沿って滑らないように転がすとき、その円の内部または外部または周上の定点\(P\)が描く軌跡をトロコイドと呼びます。
問題として扱われる場合には、\(C\)は「直線 または 円」、点\(P\)は円周上の点であることが多いです。点\(P\)は円周上の点として
(i)\(C\)が直線の場合(円が直線上を転がる)、\(P\)の軌跡はサイクロイド
(ii)\(C\)が円の場合(円が円周上を転がる)
(ア)円の外側を円が転がる場合、\(P\)の軌跡は外サイクロイド(エピサイクロイド)
特に2円の半径が同じ場合、カージオイド(心臓型)と呼ばれるハート型の曲線
(イ)円の内側を円が転がる場合、\(P\)の軌跡は内サイクロイド(ハイポサイクロイド)
特に (外側の円の半径):(転がる内側の円の半径)=4:1 の場合は、アステロイドと呼ばれる4つの尖点をもつ星型の曲線
(外側の円の半径):(転がる内側の円の半径)=2:1 の場合は、直線(線分)
と分類されます。
トロコイドの問題は、図形的処理やベクトルを用いて、点\(P\)の座標を媒介変数を用いて表すことが基本となります。座標の媒介変数表示が手に入れば、あとはただの媒介変数の積分問題になります。
またギリシャ語で、エピは上、ハイポは下という意味を持ちます。
どうでもよいかもしれませんが、ベーコンエピというパンのエピはフランス語で麦の穂という意味らしいです。
(例題)
半径\(a\)の円板が\(x\)軸上を正の方向に滑らず回転するとき、円板上の点\(P\)の描く曲線\(C\)を考える。円板の中心の最初の位置を \((0,a)\)、点\(P\)の最初の位置を 原点\(O(0,0)\) とする。円板が転がりその中心まわりに回転した角を\(θ\ [\mathrm{rad}]\)とするとき、そのときの円板と\(x\)軸との接点を\(T\)とする。
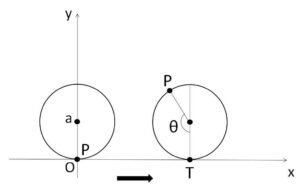
(1)\(OT\)の長さを\(θ\)を用いて表せ。
(2)\(θ\)だけ回転したときの点\(P\)の座標を求めよ。
(3)円板がちょうど1回転する際に描く点\(P\)の軌跡と\(x\)軸とで囲まれた部分の面積を求めよ。
(2)が最初の目標ですが、(1)がそのヒントになっています。
(解答)
(1)
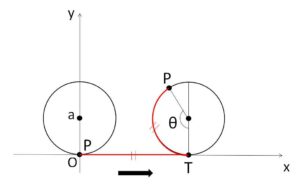
\(OT=\stackrel{\huge\frown}{TP}\) より
\(OT=aθ\)
(2)
\(\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CP}\)
です。\(\overrightarrow{OC}\) は(1)からすぐに分かり、\(\overrightarrow{CP}\) については三角関数を利用するために、\(C\)から正の方向に\(x\)軸と平行な線分を引くと、三角関数では左回りが正の方向であることから、
\(\overrightarrow{CP}=a(\cos\{-(θ+\displaystyle\frac{π}{2})\},\sin\{-(θ+\displaystyle\frac{π}{2})\})\)
となることが分かります。
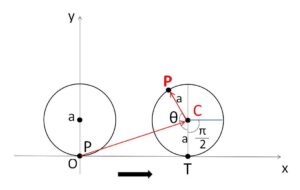
回転後の円板の中心を\(C\)とおくと、図より
\(\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CP}\)
\(=(aθ,a)+a(\cos\{-(θ+\displaystyle\frac{π}{2})\},\sin\{-(θ+\displaystyle\frac{π}{2})\})\)
\(=(aθ,a)+a(\cos(θ+\displaystyle\frac{π}{2}),-\sin(θ+\displaystyle\frac{π}{2}))\)
\(=(aθ,a)+a(-\sinθ,-\cosθ)\)
\(=(aθ-a\sinθ,\ a-a\cosθ)\)
よって
\(P(aθ-a\sinθ,\ a-a\cosθ)\)
(3)
\(P(x,y)\) とすると、\(0≦θ≦2π\) として
\(x=aθ-a\sinθ\)
\(y=a-a\cosθ\)
\(\displaystyle\frac{dx}{dθ}=a-a\cosθ=a(1-\cosθ)≧0\)
\(\displaystyle\frac{dy}{dθ}=a\sinθ\)
\(x\)は単調増加、
\(y\)は \(0≦θ≦π\) で単調増加、\(π≦θ≦2π\) で単調減少。
\(y=a-a\cosθ=0\) を満たすのは \(θ=0,2π\) で、このとき
\(x=0,2πa\)
よって\(P\)の軌跡を図示すると次のようになる。
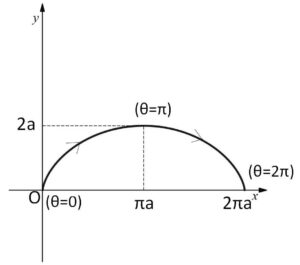
したがって面積\(S\)は
\(S=\displaystyle\int_{0}^{2πa}ydx\)
\(=\displaystyle\int_{0}^{2π}(a-a\cosθ)a(1-\cosθ)dθ\)
\(=a^2\displaystyle\int_{0}^{2π}(1-\cosθ)^2dθ\)
\(=a^2\displaystyle\int_{0}^{2π}(1-2\cosθ+\cos^2θ)dθ\)
\(=a^2\displaystyle\int_{0}^{2π}(1-2\cosθ+\displaystyle\frac{1+\cos2θ}{2})dθ\)
\(=a^2\left[\displaystyle\frac{3}{2}θ-2\sinθ+\displaystyle\frac{\sin2θ}{4}\right]_{0}^{2π}\)
\(=3πa^2\)
次回は内外サイクロイドを扱いたいと思います。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数と面積③(内外サイクロイド) back→媒介変数と面積①