極方程式で表される曲線が囲む図形の回転体の体積を求める例題です。
\(x=r\cosθ=f(θ)\cosθ\)
\(y=r\sinθ=f(θ)\sinθ\)
により媒介変数表示にします。あとはただの媒介変数表示の回転体の問題になります。
(例題)
\(xy\)平面上で原点を極、\(x\)軸の正の部分を始線とする極座標に関して、極方程式
\(r=2+\cosθ\) (\(0≦θ≦π\))
により表される曲線を\(C\)とする。\(C\)と\(x\)軸とで囲まれた図形を\(x\)軸のまわりに1回転して得られる立体の体積を求めよ。
(解答)
\(r=2+\cosθ\) (\(0≦θ≦π\)) より
\(x=(2+\cosθ)\cosθ\)
\(y=(2+\cosθ)\sinθ\)
\(\displaystyle\frac{dx}{dθ}=-\sinθ\cosθ+(2+\cosθ)(-\sinθ)\)
\(=-2\sinθ(\cosθ+1)≦0\) (単調減少)
\(\displaystyle\frac{dy}{dθ}=-\sinθ\sinθ+(2+\cosθ)\cosθ\)
\(=\cos^2θ-1+2\cosθ+\cos^2θ\)
\(=2\cos^2θ+2\cosθ-1\)
\(\displaystyle\frac{dy}{dθ}=0\) のとき
\(\cosθ=\displaystyle\frac{-1±\sqrt{3}}{2}\) (\(-\)のほうは\(\cosθ<-1\)となり不適)
\(\cosθ=\displaystyle\frac{-1+\sqrt{3}}{2}\) を満たす\(θ\)を\(α\)とおくと、
\(0≦θ≦α\) で\(y\)は単調増加、\(α≦θ≦π\) で\(y\)は単調減少。
また、\(θ=0,π\) のときそれぞれ \(x=3,-1\)、\(y=0,0\) となるので、曲線\(C\)のグラフは次の通り。
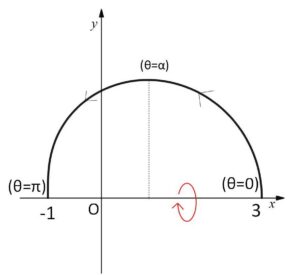
よって体積\(V\)は、\(dx=-2\sinθ(\cosθ+1)dθ\) より
\(V=π\displaystyle\int_{-1}^{3}y^2dx\)
(置換積分。積分区間の対応に注意)
\(=π\displaystyle\int_{π}^{0}(2+\cosθ)^2\sin^2θ\cdot(-2)\sinθ(\cosθ+1)dθ\)
(\(\sinθ\)を1つ残すと、導関数接触型)
\(=2π\displaystyle\int_{π}^{0}(2+\cosθ)^2(1-\cos^2θ)(\cosθ+1)(-\sinθ)dθ\)
(\(\cosθ=t\) で置換)
\(=2π\displaystyle\int_{-1}^{1}(2+t)^2(1-t^2)(t+1)dt\)
\(=2π\displaystyle\int_{-1}^{1}(-t^4-4t^3-3t^2+4t+4)(t+1)dt\)
(偶奇関数の定積分。奇数乗は\(0\)になる)
\(=4π\displaystyle\int_{0}^{1}(-5t^4+t^2+4)dt\)
\(=4π\left[-t^5+\displaystyle\frac{1}{3}t^3+4t\right]_{0}^{1}\)
\(=\displaystyle\frac{40}{3}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→x,y軸に平行な直線に関する回転体 back→媒介変数表示と回転体