2次方程式が異なる2つの実数解をもち、解が2つとも特定の区間にある条件を考えていきます。今までの知識((8-1)~(8-4))を応用させます。
(問題)
2次方程式 \(x^2-2(a+1)x+3a=0\) が、\(-1≦x≦3\)の範囲に異なる2つの実数解をもつような定数\(a\)の値の範囲を求めよ。
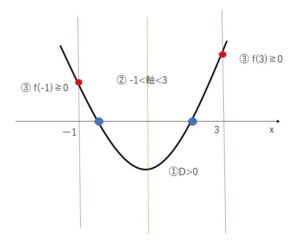
左辺を\(f(x)\)とおくと、グラフが\(x\)軸の \(-1≦x≦3\) の範囲において2点で交わる条件を求めます。 ①判別式 ②軸 ③端 の3つに着目します。解が\(-1\)、\(3\) でもよいので、端の\(f(-1)\)と\(f(3)\)の条件の不等号にはイコールがつきます。
(解答)
\(f(x)=x^2-2(a+1)x+3a\) とおく。題意を満たす条件は、\(y=f(x)\)のグラフが \(x\)軸の \(-1≦x≦3\) の範囲で異なる2点で交わることである。よって次の条件すべてが成り立つ場合である。
\(f(x)=x^2-2(a+1)x+3a\) とおく。題意を満たす条件は、\(y=f(x)\)のグラフが \(x\)軸の \(-1≦x≦3\) の範囲で異なる2点で交わることである。よって次の条件すべてが成り立つ場合である。
(1)判別式 \(D>0\)
(2)軸について \(-1<a+1<3\)
(3)端について \(f(-1)≧0\) \(f(3)≧0\)
(2)軸について \(-1<a+1<3\)
(3)端について \(f(-1)≧0\) \(f(3)≧0\)
(1)\(\displaystyle\frac{D}{4}=\{-(a+1)\}^2-3a\)
\(=a^2-a+1=(a-\displaystyle\frac{1}{2})^2+\displaystyle\frac{3}{4}\)
よって \(D>0\)は常に成り立つ。
\(=a^2-a+1=(a-\displaystyle\frac{1}{2})^2+\displaystyle\frac{3}{4}\)
よって \(D>0\)は常に成り立つ。
(2)\(-1<a+1<3\) より \(-2<a<2\)・・・①
(3)\(f(-1)=5a+3≧0\) より \(a≧-\displaystyle\frac{3}{5}\)・・・②
\(f(3)=-3a+3≧0\) より \(a≦1\)・・・③
\(f(3)=-3a+3≧0\) より \(a≦1\)・・・③
①~③の共通部分を求めると
\(-\displaystyle\frac{3}{5}≦a≦1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。