複素数の積・商が複素数平面上でどのような挙動をするか見ていきます。
・複素数の積・商と回転・縮小拡大
複素数の極形式と三角関数の加法定理を利用することにより、複素数の積・商の複素数平面での挙動を調べることができます。
まず積からですが、\(0\)でない2つの複素数\(z_1,z_2\)の極形式を
\(z_1=r_1(\cosθ_1+i\sinθ_1)\)、\(z_2=r_2(\cosθ_2+i\sinθ_2)\) (\(r_1>0,\ r_2>0\))
とおいて、積\(z_1z_2\)を求めると
\(z_1z_2=r_1r_2(\cosθ_1+i\sinθ_1)(\cosθ_2+i\sinθ_2)\)
(実部と虚部で分けて)
\(=r_1r_2\{(\cosθ_1\cosθ_2-\sinθ_1\sinθ_2)+i(\sinθ_1\cosθ_2+\cosθ_1\sinθ_2)\}\)
よって加法定理の展開の逆の操作をすることにより
\(z_1z_2=r_1r_2\{\cos(θ_1+θ_2)+i\sin(θ_1+θ_2)\}\)・・・①
と極形式の形になり、\(z_1z_2\)の絶対値は\(r_1r_2\)、偏角(の1つは) \(θ_1+θ_2\) となるので次のことが成り立ちます。
\(|z_1z_2|=r_1r_2\)・・・②
\(\arg(z_1z_2)=\arg z_1+\arg z_2\)・・・③
偏角の公式③が意味するのは、積の偏角はもとの2つの偏角の和になるということで、これについては注意点がいくつかあるのですが後述することにして、まず①の図形的意味を考えてみます。
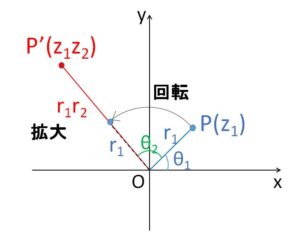
積\(z_1z_2\)を \(z_1\)に\(z_2\)を掛けると見ると、複素数平面上において\(P(z_1)\)から見て\(P'(z_1z_2)\)がどの位置にあるかというと①の右辺の形から
「点\(P(z_1)\)を原点の周りに\(θ_2\)だけ回転させて、原点からの距離を\(r_2\)倍に拡大縮小した位置にある」
ことが分かります。つまり複素数の積は図形的には次の2つの操作の組み合わせとなります。
(i)回転移動 (ii)拡大縮小
したがって特に \(r_2=1\) とすると回転移動だけになり、複素数平面や座標平面での回転移動を考えるときに複素数の積がよく利用されます。
(偏角の公式③の注意点)
\(\arg(z_1z_2)=\arg z_1+\arg z_2\)・・・③ について、以下の点に注意してください。
(1)偏角を \(0≦θ<2π\) に限定すると③は成り立たなくなる場合があるので、一般角でとる。
(2)\(2nπ\) (\(n\)は整数) の違いだけなら③は成り立つことにする。
(1)について
例えば、\(z_1=-i\)、\(z_2=1-i\) として範囲を限定すると
\(z_1z_2=-1-i\) より \(\arg(z_1z_2)=\displaystyle\frac{5π}{4}\)
ところが、\(\arg z_1=\displaystyle\frac{3π}{2}\)、\(\arg z_2=\displaystyle\frac{7π}{4}\) だから、\(\arg(z_1z_2)≠\arg z_1+\arg z_2\)
よってこのような場合でも成り立たせるために一般角でとる必要がある。
(2)について
しかし一般角でとると、偏角の取り方は無数に存在するために等式③が成り立たない(ぴったり両辺の角が等しくならない)場合がでてくる。それでは不便なので、\(2nπ\) のズレなら等しいものとして扱うことにする。\(2nπ\)のズレなら複素数の表す点の位置は同じなので、こうしてもさして問題にならない。すると、上記\(z_1,z_2\)では
\(\displaystyle\frac{5π}{4}+(2π)=\displaystyle\frac{3π}{2}+\displaystyle\frac{7π}{4}\)
となり、偏角の等式③が成り立つことになる。
結局のところ、一般角でとっても\(2nπ\)のズレしか生じないので、(2)だけを気を付ければよいことになります。
次に複素数の商ですが、ほとんど積と同様なのでざっくりとした説明にしておきます。
\(0\)でない2つの複素数\(z_1,z_2\)の極形式を
\(z_1=r_1(\cosθ_1+i\sinθ_1)\)、\(z_2=r_2(\cosθ_2+i\sinθ_2)\) (\(r_1>0,\ r_2>0\))
とおいて、商\(\displaystyle\frac{z_1}{z_2}\)を求めると
\(\displaystyle\frac{z_1}{z_2}=\displaystyle\frac{r_1(\cosθ_1+i\sinθ_1)}{r_2(\cosθ_2+i\sinθ_2)}\)
(分母を実数化して)
\(=\displaystyle\frac{r_1}{r_2}\cdot\displaystyle\frac{(\cosθ_1+i\sinθ_1)(\cosθ_2-i\sinθ_2)}{(\cos^2θ_2+\sin^2θ_2)}\)
\(=\displaystyle\frac{r_1}{r_2}\{(\cosθ_1\cosθ_2+\sinθ_1\sinθ_2)+i(\sinθ_1\cosθ_2-\cosθ_1\sinθ_2)\}\)
(加法定理により)
\(=\displaystyle\frac{r_1}{r_2}\{\cos(θ_1-θ_2)+i\sin(θ_1-θ_2)\}\)・・・④ (商の極形式)
よって複素数の商では、\(z_1\)の絶対値\(r_1\)を\(\displaystyle\frac{1}{r_2}\)倍して、\(θ_1\)から\(θ_2\)を引けばよいことになります。つまり
\(\left|\displaystyle\frac{z_1}{z_2}\right|=\displaystyle\frac{r_1}{r_2}\)・・・⑤
\(\arg(\displaystyle\frac{z_1}{z_2})=\arg z_1-\arg z_2\)・・・⑥
偏角の公式⑥は一般角でとることと、\(2nπ\)のズレなら成り立つことにするのは積と同様です。
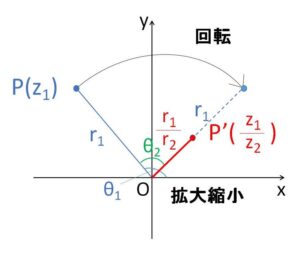
また、商の極形式④の図形的意味は\(z_1\)から見ると
「点\(P(z_1)\)を原点の周りに\(-θ_2\)だけ回転させて、原点からの距離を\(\displaystyle\frac{1}{r_2}\)倍に拡大縮小した位置に\(P'(\displaystyle\frac{z_1}{z_2})\)がある」
です。(回転+拡大縮小)
(例題)
\(\displaystyle\frac{\sqrt{3}+i}{1-i}\) を極形式で表せ。ただし偏角\(θ\)は、\(0≦θ<2π\) とする。
(解答)
\(\displaystyle\frac{\sqrt{3}+i}{1-i}\)
(先に分母分子を極形式表示にする)
\(=\displaystyle\frac{2(\cos\displaystyle\frac{π}{6}+i\sin\displaystyle\frac{π}{6})}{\sqrt{2}(\cos\displaystyle\frac{7π}{4}+i\sin\displaystyle\frac{7π}{4})}\)
\(=\sqrt{2}\{\cos(\displaystyle\frac{π}{6}-\displaystyle\frac{7π}{4})+i\sin(\displaystyle\frac{π}{6}-\displaystyle\frac{7π}{4})\}\)
\(=\sqrt{2}\{\cos(-\displaystyle\frac{19π}{12})+i\sin(-\displaystyle\frac{19π}{12})\}\)
\(=\sqrt{2}(\cos\displaystyle\frac{5π}{12}+i\sin\displaystyle\frac{5π}{12})\)
(注)
偏角が指定された範囲に入っていない場合には、解答のように\(2nπ\)だけずらして入るようにすればよい。また分母の偏角を\(-\displaystyle\frac{π}{4}\)にすると楽になる。
なお先に実数化して最後に極形式表示にしようとすると、\(\displaystyle\frac{5π}{12}\) (\(75°\)) の三角比を知らないと答えが出ない。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ある点まわりの回転 back→複素数の極形式