原点以外のある点まわりの回転の仕方について見ていきます。
・ある点まわりの回転
複素数平面上で 点\(α\) のまわりに回転させるには、全体を\(-α\)だけ平行移動させて原点まわりの回転に帰着させればよいです。
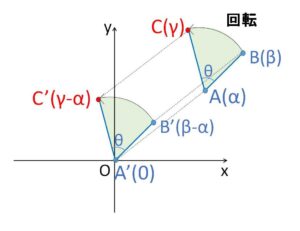
すなわち、点\(B(β)\)を点\(A(α)\)まわりに\(θ\)だけ回転した後の点を\(C(γ)\)とすると、全体を\(-α\)だけ平行移動した後の点をそれぞれ
「\(B'(β-α)\)、\(A'(0)\) (原点)、\(C'(γ-α)\)、」
とすると、原点まわりに\(B’\)を\(θ\)だけ回転すると\(C’\)になるので
\(γ-α=(β-α)(\cosθ+i\sinθ)\)・・・①
(\(γ\)を具体的に求める場合は移項して)
\(γ=(β-α)(\cosθ+i\sinθ)+α\)
となります。
または次のように考えて①を導くこともできます。\(A(α)\)をあたかも原点のように扱って、複素数の和・差はベクトルの性質をもつことから
\(\overrightarrow{AB}\)を表す複素数は \(β-α\)
\(\overrightarrow{AC}\)を表す複素数は \(γ-α\)
であり、\(\overrightarrow{AB}\)を\(θ\)だけ回転すると\(\overrightarrow{AC}\)になるから
\(γ-α=(β-α)(\cosθ+i\sinθ)\)・・・①
と結論づけることもできます。ベクトルが位置を気にしないように、複素数の和・差も位置を気にしない向きと大きさを表す量です。
(例題)
2つの複素数
\(α=-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\), \(β=-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
がある。複素数平面上で、点\(β\)を中心として、点\(α\)を時計回りに\(135°\)回転させたときの点を表す複素数\(γ\)を求めよ。
(解答)
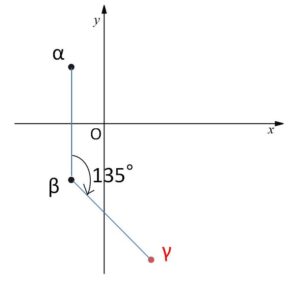
\(α=-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\), \(β=-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
題意より
\(γ-β=(α-β)\{\cos(-\displaystyle\frac{3π}{4})+i\sin(-\displaystyle\frac{3π}{4})\}\) だから
\(γ=\sqrt{3}i(-\displaystyle\frac{1}{\sqrt{2}}-\displaystyle\frac{1}{\sqrt{2}}i)+(-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i)\)
よって
\(γ=\displaystyle\frac{\sqrt{6}-1}{2}-\displaystyle\frac{\sqrt{6}+\sqrt{3}}{2}i\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数平面と三角関数 back→複素数の積・商と回転