複素数を利用した図形の証明問題です。
(例題)
図のように、複素数平面上に四角形\(ABCD\)があり、4点\(A,B,C,D\)を表す複素数をそれぞれ\(z_1,z_2,z_3,z_4\)とする。各辺を1辺とする4つの正方形\(BAPQ\)、\(CBRS\)、\(DCTU\)、\(ADVW\)を四角形\(ABCD\)の外側に作り、正方形\(BAPQ\)、\(CBRS\)、\(DCTU\)、\(ADVW\)の中心をそれぞれ\(K,L,M,N\)とおく。
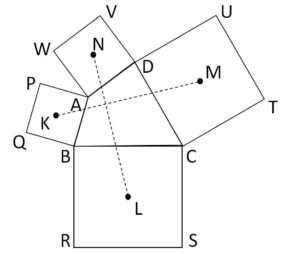
(1)点\(K\)を表す複素数\(ω_1\)を\(z_1,z_2\)で表せ。
(2)\(KM=LN\)、\(KM \perp LN\) を証明せよ。
(3)線分\(KM\)と線分\(LN\)の中点が一致するのは四角形\(ABCD\)がどのような図形のときか。
(解答)
(1)
または、直接\(K\)を\(45°\)回転と拡大縮小より求めることもできます。
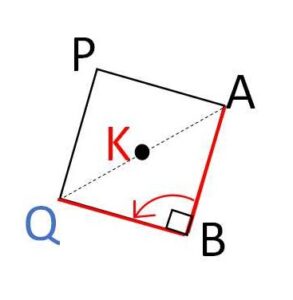
\(Q(q)\)とおくと、\(B(z_2)\)まわりに\(A(z_1)\)を\(\displaystyle\frac{π}{2}\)だけ回転した点が\(Q\)だから
\(q=(z_1-z_2)(\cos\displaystyle\frac{π}{2}+i\sin\displaystyle\frac{π}{2})+z_2\)
よって
\(q=i(z_1-z_2)+z_2\)
\(K(ω_1)\)は\(AQ\)の中点だから
\(ω_1=\displaystyle\frac{z_1+i(z_1-z_2)+z_2}{2}\)
\(=\displaystyle\frac{1+i}{2}z_1+\displaystyle\frac{1-i}{2}z_2\)
(別解)
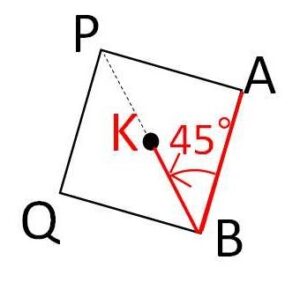
正方形の1辺の長さを\(1\)とすると、対角線の長さは\(\sqrt{2}\)。よって\(BK\)の長さは\(\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{1}{\sqrt{2}}\)
したがって、\(B(z_2)\)まわりに\(A(z_1)\)を\(\displaystyle\frac{π}{4}\)だけ回転し\(\displaystyle\frac{1}{\sqrt{2}}\)倍した点が\(K(ω_1)\)だから
\(ω_1=(z_1-z_2)\cdot\displaystyle\frac{1}{\sqrt{2}}(\cos\displaystyle\frac{π}{4}+i\sin\displaystyle\frac{π}{4})+z_2\)
\(=\displaystyle\frac{1+i}{2}z_1+\displaystyle\frac{1-i}{2}z_2\)
(2)
まず\(L\)については、\(C\)まわりに\(B\)を反時計回りに回転することになるので、\(A(z_1) \to B(z_2)\)、\(B(z_2) \to C(z_3)\)の対応関係になり、(1)の結果で \(z_1 \to z_2\)、\(z_2 \to z_3\) とすればよいだけです。
\(M,N\)も同様です。
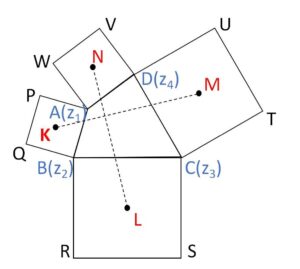
\(L(ω_2)\) とおくと、(1)の結果で \(z_1 \to z_2\)、\(z_2 \to z_3\) とすると
\(ω_2=\displaystyle\frac{1+i}{2}z_2+\displaystyle\frac{1-i}{2}z_3\)
同様に \(M(ω_3),N(ω_4)\) とおくと
\(ω_3=\displaystyle\frac{1+i}{2}z_3+\displaystyle\frac{1-i}{2}z_4\)
\(ω_4=\displaystyle\frac{1+i}{2}z_4+\displaystyle\frac{1-i}{2}z_1\)
\(\displaystyle\frac{ω_4-ω_2}{ω_3-ω_1}=±i\)
(\(ω_4-ω_2=±i(ω_3-ω_1\))
が成り立つはずです。\(±i\)はどちらか一方が成り立っていればよいという意味です。図から判断すると恐らく\(+i\)になるはずです。
よって
\(ω_3-ω_1=\displaystyle\frac{1+i}{2}z_3+\displaystyle\frac{1-i}{2}z_4-\left(\displaystyle\frac{1+i}{2}z_1+\displaystyle\frac{1-i}{2}z_2\right)\)
\(=\displaystyle\frac{-z_1-z_2+z_3+z_4}{2}+\displaystyle\frac{-z_1+z_2+z_3-z_4}{2}i\)
\(ω_4-ω_2=\displaystyle\frac{1+i}{2}z_4+\displaystyle\frac{1-i}{2}z_1-\left(\displaystyle\frac{1+i}{2}z_2+\displaystyle\frac{1-i}{2}z_3\right)\)
\(=\displaystyle\frac{z_1-z_2-z_3+z_4}{2}+\displaystyle\frac{-z_1-z_2+z_3+z_4}{2}i\)
ゆえに
\(ω_4-ω_2=i(ω_3-ω_1)\)
が成り立つので、\(\overrightarrow{KM}\)を\(\displaystyle\frac{π}{2}\)だけ回転させると\(\overrightarrow{LN}\)となる(ベクトルの始点を合わせて始点まわりの回転をさせる)。
したがって
\(KM=LN\)、\(KM \perp LN\)
が成り立つ。
(3)
(1)(2)より
\(ω_1=\displaystyle\frac{1+i}{2}z_1+\displaystyle\frac{1-i}{2}z_2\)
\(ω_2=\displaystyle\frac{1+i}{2}z_2+\displaystyle\frac{1-i}{2}z_3\)
\(ω_3=\displaystyle\frac{1+i}{2}z_3+\displaystyle\frac{1-i}{2}z_4\)
\(ω_4=\displaystyle\frac{1+i}{2}z_4+\displaystyle\frac{1-i}{2}z_1\)
線分\(KM\)と線分\(LN\)の中点が一致するとき
\(\displaystyle\frac{ω_1+ω_3}{2}=\displaystyle\frac{ω_2+ω_4}{2}\)
\(2(ω_1+ω_3)=2(ω_2+ω_4)\)
\((1+i)z_1+(1-i)z_2+(1+i)z_3+(1-i)z_4\)
\(=(1-i)z_1+(1+i)z_2+(1-i)z_3+(1+i)z_4\)
整理して
\(2i(z_1-z_2+z_3-z_4)=0\)
よって
\(z_1-z_2+z_3-z_4=0\)・・・①
①より
\(z_1-z_2=z_4-z_3\)
したがって、\(\overrightarrow{BA}=\overrightarrow{CD}\) だから、四角形\(ABCD\)は平行四辺形。
(参考)
①の和の部分に着目して
\(z_1+z_3=z_2+z_4\)
よって
\(\displaystyle\frac{z_1+z_3}{2}=\displaystyle\frac{z_2+z_4}{2}\)
より、対角線の中点が一致するとして平行四辺形と判断してもよい。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の方程式 back→三角形の形状