絶対値を含む2次方程式と2次不等式を解いていきます。解き方には、数式変形だけで解く方法とグラフを利用する方法があります。
(例題1)次の方程式を解け。
\(|x^2-4|=-3x\)
(解答)
\(x^2-4=(x+2)(x-2)\)より
①\(x≦-2\) または \(x≧2\) のとき
\(x^2-4=-3x\) これを解くと \((x+4)(x-1)=0\) より
\(x=-4,1\) よって解は \(x=-4\)
②\(-2<x<2\) のとき
\(-(x^2-4)=-3x\) これを解くと \((x+1)(x-4)=0\) より
\(x=-1,4\) よって解は \(x=-1\)
①②より 解は \(x=-4,-1\)
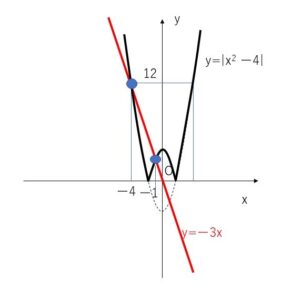
\(y=\)(左辺) と \(y=\)(右辺) のグラフを書くと下図になります。
交点の\(x\)座標が解となります。
(例題2)次の不等式を解け。
\(|x^2-2x-3|≧3-x\)
(解答)
\(x^2-2x-3=(x+1)(x-3)\) より
①\(x≦-1\) または \(x≧3\) ・・・(a) のとき
\(x^2-2x-3≧3-x\) これを解くと
\(x^2-x-6≧0\) \((x+2)(x-3)≧0\) より
\(x≦-2\) または \(x≧3\) これは (a)を満たす
②\(-1<x<3\) ・・・(b) のとき
\(-(x^2-2x-3)≧3-x\) これを解くと
\(x^2-2x-3≦x-3\) \(x(x-3)≦0\) より
\(0≦x≦3\) (b)を満たすのは \(0≦x<3\)
①②より不等式の解は \(x≦-2\) または \(x≧0\)
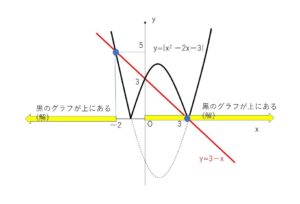
\(y=\)(左辺) と \(y=\)(右辺) のグラフを書くと下図になります。
左辺のグラフが右辺のグラフより上側(同じでもよい)にある\(x\)の範囲が解となります。
以上になります。お疲れ様でした。
ここまで読んで下さりありがとうございました。