2つの放物線 \(y=f(x)\)と \(y=g(x)\) の共有点の座標は、共有点\((x,y)\)が2式を同時に満たすことから、連立方程式 \(y=f(x)\),\(y=g(x)\) を解くことで求めることができます。ただし実数解をもたない(共有点がない)場合もあります。
(例題1)次の2つの放物線は共有点をもつか。もつ場合にはその座標を求めよ。
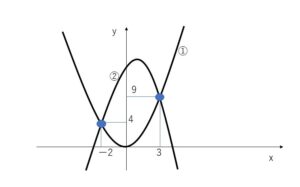
(1)\(y=x^2\)・・・① \(y=-x^2+2x+12\)・・・②
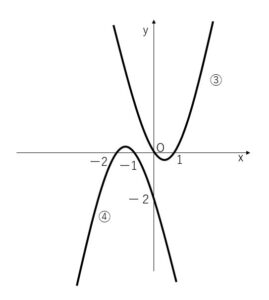
(2)\(y=x^2-x\)・・・③ \(y=-x^2-3x-2\)・・・④
(解答)
(1)
①②から\(y\)を消去して、
\(x^2=-x^2+2x+12\) \(x^2-x-6=0\) より
\((x+2)(x-3)=0\) よって \(x=-2,3\)
①に代入して\(y\)を求めると、共有点の座標は
\((-2,4),(3,9)\)
(2)
③④から\(y\)を消去して
\(x^2-x=-x^2-3x-2\) よって
\(x^2+x+1=0\)
この2次方程式の判別式について \(D=1-4=-3<0\) であり
この2次方程式は実数解をもたない。したがって2つの放物線③④は共有点をもたない。
(例題2)次の2つの放物線の共有点の座標を求めよ。
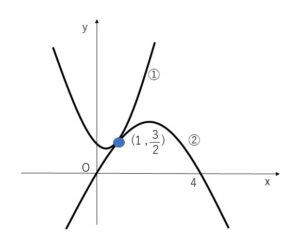
(1)\(y=x^2-x+\displaystyle\frac{3}{2}\)・・・① \(y=-\displaystyle\frac{1}{2}x^2+2x\)・・・②
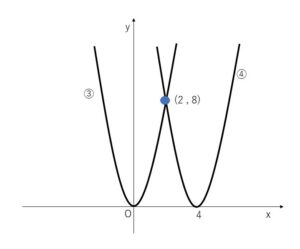
(2)\(y=2x^2\)・・・③ \(y=2(x-4)^2\)・・・④
(解答)
(1)
①②から\(y\)を消去して
\(x^2-x+\displaystyle\frac{3}{2}=-\displaystyle\frac{1}{2}x^2+2x\)
整理して
\(x^2-2x+1=0\) \((x-1)^2=0\)
よって \(x=1\) (重解)
①に代入して \(y=\displaystyle\frac{3}{2}\)
したがって 共有点の座標は \((1,\displaystyle\frac{3}{2})\)
③④から\(y\)を消去して
\(2x^2=2(x-4)^2\) 整理すると
\(0=-8x+16\) よって
したがって 共有点の座標は \((2,8)\)
ここまで見て頂きありがとうございました。