正規分布の標準化について見ていきます。
・標準正規分布
\(X\)が期待値\(m\)、分散\(σ^2\)の正規分布に従うとき、確率密度関数は
\(f(x)=\displaystyle\frac{1}{\sqrt{2π}σ}e^{-\frac{(x-m)^2}{2σ^2}}\)・・・①
で表されましたが、\(m,σ^2\)が変化する分だけ無数に正規分布が存在し、この関数と\(x\)軸の間の面積(確率)を逐一計算したり調べたりするのは大変です。
そこで変数変換を行うことで、「期待値\(0\)、分散\(1\)」の\(y\)軸対称の単純な正規分布にするという操作を行います。この操作を正規分布の標準化とよび、標準化された正規分布を標準正規分布とよびます。
変数変換の公式
\(E(X-k_1)=E(X)-k_1\)、\(V(k_2X)=k_2^2V(X)\)
を考えると、\(E(X)=m\)、\(V(X)=σ^2\) の分布を「期待値\(0\)、分散\(1\)」にするには、
\(k_1=m\)、\(k_2=\displaystyle\frac{1}{σ}\)
とすればよいので、\(X\)を次のように変数変換すればよいことが分かります。
\(Z=\displaystyle\frac{X-m}{σ}\) (標準化の変数変換)
(平均値を引いて標準偏差で割ればよいということ)
実際
\(E(Z)=E(\displaystyle\frac{X-m}{σ})=E(\displaystyle\frac{X}{σ}-\displaystyle\frac{m}{σ})\)
\(=\displaystyle\frac{1}{σ}E(X)-\displaystyle\frac{m}{σ}=0\)
\(V(X)=V(\displaystyle\frac{X-m}{σ})=V(\displaystyle\frac{X}{σ}-\displaystyle\frac{m}{σ})\)
\(=\displaystyle\frac{1}{σ^2}V(X)=1\)
であり、これで任意の正規分布が標準正規分布に変換できることになります。
なお上記変数変換ではグラフ上では平行移動と拡大縮小しか行っていないことになるので確率変数\(Z\)も同様に正規分布に従い、\(Z\)は標準正規分布 \(N(0,1)\) に従うことになります。
また、標準正規分布の確率密度関数は①で \(m=0\)、\(σ^2=1\) (\(σ=1\)) とし、変数を\(z\)に変えることで得られます。
\(f(z)=\displaystyle\frac{1}{\sqrt{2π}}e^{-\frac{z^2}{2}}\)・・・②
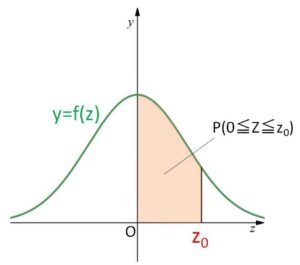
この確率密度関数と\(x\)軸とで囲まれる面積(確率)
\(P(0≦Z≦z_0)=p(z_0)\)
\(=\displaystyle\int_{0}^{z_0}f(z)dz\)
は調べ尽くされていて、それをまとめた下記表を正規分布表とよびます。
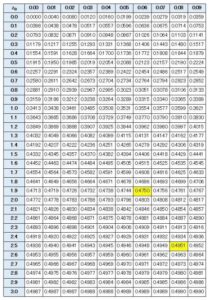
例えば黄色く表示したうちの1つ
\(z_0=1.96\)
では、\(P(0≦Z≦1.96)=0.475\) (確率\(47.5%\)) より
\(\displaystyle\int_{0}^{1.96}f(z)dz=0.475\)
であることが分かり、逆に
\(P(0≦Z≦z_0)=0.475\)
を満たす\(z_0\)は、\(z_0=1.96\) であると表から判断することが可能です。
この表では、右内側 \(0≦z≦z_0\) の範囲の面積(確率)しか表記されていませんが、標準正規分布のグラフの\(y\)軸対称性などを利用して、左側の方の面積や、\(z≧z_0\) のような外側の面積も求めることができます。
黄色く表示した、\(z_0=1.96\) と \(z_0=2.58\) は統計的な推測でとてもよく使う値ですが、これらについて\(y\)軸対称性を利用すると、
\(P(-1.96≦Z≦1.96)=\displaystyle\int_{-1.96}^{1.96}f(z)dz\)
\(=0.475×2=0.95\) (確率\(95%\))
\(P(-2.58≦Z≦2.58)=\displaystyle\int_{-2.58}^{2.58}f(z)dz\)
\(=0.495×2=0.99\) (確率\(99%\))
となることが分かります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→正規分布に関する例題 back→正規分布