放物線と円の共有点(放物線と円が接する)についての例題です。
一般に、\(n\)次関数どうしの場合には「接する \(⇔\) 重解」という条件が使えますが、円が絡む場合には「重解 \(→\) 接する」(ただし実数条件には注意) という条件になるので、重解をもたずに接する場合もあります。
(例題1)
放物線: \(y=\displaystyle\frac{1}{2}x^2\)
円: \(x^2+(y-p)^2=9\)
がある。ただし\(p\)は定数とする。
(1)放物線と円の共有点の個数を調べよ。
(2)放物線と円が接するときの\(p\)の値を求めよ。
円の中心の\(y\)座標が動くので、固定された放物線に対して円が上下に動くことになり\(p\)の値により共有点の個数が変化します。
特に、円が放物線の上側から降りてくるときにどのように共有点をもつかが重要です。放物線の容器に円を落として「ひっかかるか、ひっかからずに原点まで落ちるか」を検討します。(例題1)ではひっかかる、(例題2)ではひっかからないケースですが、これは2つの方程式から1文字を消去した数式処理で判明します。
文字消去は\(x\)を消去したほうが\(y\)の2次式になり楽です。ただし、\(y=\displaystyle\frac{1}{2}x^2\) より、\(y\)は\(0\)以上の値でないと\(x\)が虚数になってしまう(この場合は共有点はない)ことと、\(y\)が\(0\)より大きい値の場合は対応する\(x\)は2つあることに気を付けてください。
(解答)
(1)
\(y=\displaystyle\frac{1}{2}x^2\)・・・①
\(x^2+(y-p)^2=9\)・・・②
①より \(x^2=2y\)・・・③
③を②に代入して
\(2y+(y-p)^2=9\)
整理すると
\(y^2-2(p-1)y+p^2-9=0\)・・・④
\(y>0\) のとき \(y\)1つで実数\(x\)は2つ→共有点2個
\(y=0\) のとき \(y\)1つで実数\(x\)は1つ→共有点1個
\(y<0\) のとき \(y\)1つで実数\(x\)は0つ→共有点0個
の対応になるので、④の解\(y\)の正負が\(p\)でどう変わるか調べます。\(p\)は簡単に分離できそうにないので、④のままの形で場合分けして調べます。
④の
\(\displaystyle\frac{D}{4}=(p-1)^2-(p^2-9)\)
\(=-2(p-5)\)
(i)\(D<0\) のとき
\(p>5\) であり、このとき\(y\)は虚数となるので共有点なし。
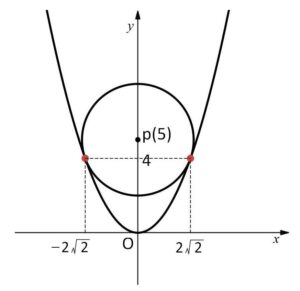
(ii)\(D=0\) のとき
\(p=5\) であり、このとき重解は
\(y=p-1=4>0\) だから③より対応する\(x\)は \(x=±2\sqrt{2}\) の2つ。
よって共有点は2つ。
(iii)\(D>0\) のとき
\(p<5\) であり、④の左辺の2次関数の\(y=0\)による値でさらに場合分けすると
\(p^2-9=0\) のとき \(p=±3\) だから、軸\(p-1\)も考慮して④の解はそれぞれ
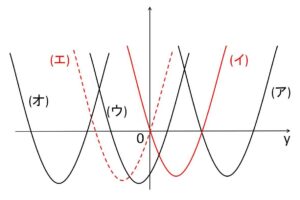
(ア)\(3<p<5\) のとき
\(y>0\) の異なる解を2つもつ。よって対応する実数\(x\)は合計4つなので、共有点は4つ。
(イ)\(p=3\) のとき
\(y=0\) の解と \(y>0\) の解を1つずつもつ。よって対応する実数\(x\)は合計3つなので、共有点は3つ。
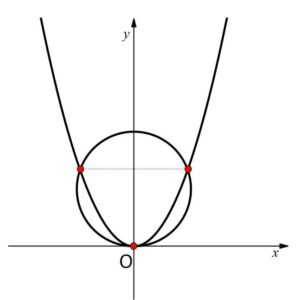
(ウ)\(-3<p<3\) のとき
\(y>0,\ y<0\) の解を1つずつもつので、対応する実数\(x\)は合計2つ。よって共有点は2つ。
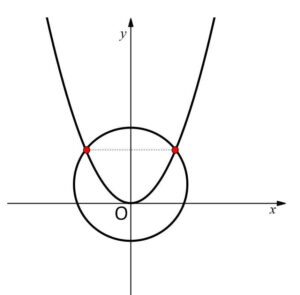
(エ)\(p=-3\) のとき
\(y=0\) と \(y<0\) の解と1つずつもつので、対応する実数\(x\)は合計1つ。よって共有点は1つ。
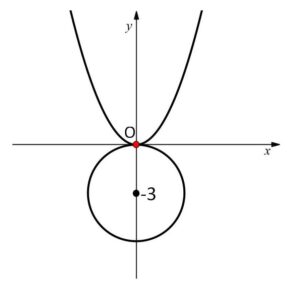
(オ)\(p<-3\) のとき
\(y<0\) の異なる解を2つもつので、対応する実数\(x\)はない。よって共有点は\(0\)つ。
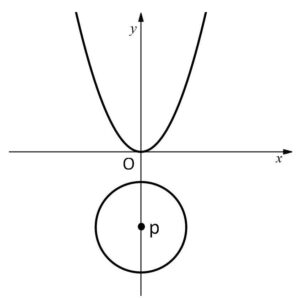
以上をまとめると
\(p>5\) のとき 共有点なし
\(p=5\) のとき 2つ
\(3<p<5\) のとき 4つ
\(p=3\) のとき 3つ
\(-3<p<3\) のとき 2つ
\(p=-3\) のとき 1つ
\(p<-3\) のとき 共有点なし
結局ポイントになったのは、重解をもつ場合(\(0\)以上の解になるかは確認必要)と原点で交わっている(円の上端or下端で接している)場合なので、これら\(p=5,3,-3\)を境界として円を動かしてどう共有点が変化するか調べてもよいです。個数がどうなるか微妙なときはその場合のみ上記のように方程式で調べればよいです。
(2)
原点で放物線は\(x\)軸に接していて、円の上端と下端の接線は\(x\)軸に平行であることに注意すると、(1)の結果と図より2曲線が接するとき
\(p=5,3,-3\)
(内訳)
\(p=5\) では2点で接する
\(p=3\) では1点(原点)で接し、他2点で交わる
\(p=-3\) では1点(原点)で接し、他の共有点はない。
(参考1)
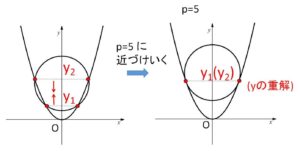
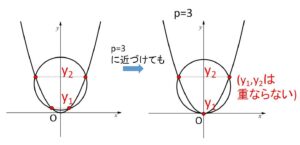
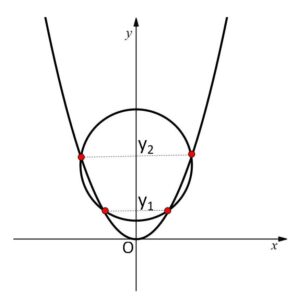
重解により判明する接する条件は \(p=5\) のみで、\(p=±3\) は出てきません。これは重解が異なる2つの解が重なる瞬間であるからです。\(p=5\) の場合は \(3<p<5\) の場合の異なる2解\(y_1,y_2\)が\(p=5\)に近づくにつれて近づき、\(p=5\)になると\(y_1,y_2\)が重なるつまり重解になります。一方例えば\(p=3\)では、\(3<p<5\) の場合の2解\(y_1,y_2\)は\(p=3\)に近づくにつれても近づかずに、\(p=3\)で重なりません。
ただし、この理屈の通り\(x\)方向に着目すると異なる\(x\)が重なるので、\(y\)消去の\(x\)の方程式にすれば原点で接する場合についても重解で出てきます。(ただし4次方程式の処理にはなります)
この例のように一方の方程式が円のような\(n\)次関数になってない場合には、「重解 \(⇔\) 接する」とはなっておらず、また重解であっても実数条件(\(x\)が実数でとれるか)を考慮する必要があり、(例題2)のように却下されることもあるので慎重に検討する必要があります。
(参考2)
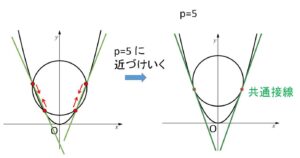
微分では、2曲線が接するとは「ある共有点をもち、その共有点での接線が一致する」と定義します。接線は曲線上の2点を通る直線において、この2点を近づけたときの極限状態です。2曲線の交点を通る直線を考えれば、\(p=5\) の場合に2曲線は共通接線を持つ(2本)ことが分かり、この定義と合致します。
原点で接する \(p=±3\) の場合には\(x\)軸が共通接線になっているのはよいでしょう。
(例題2)
放物線: \(y=\displaystyle\frac{1}{8}x^2\)
円: \(x^2+(y-p)^2=9\)
がある。ただし\(p\)は定数とする。
(1)放物線と円の共有点の個数を調べよ。
(2)放物線と円が接するときの\(p\)の値を求めよ。
(解答)
(1)
\(y=\displaystyle\frac{1}{8}x^2\)・・・①
\(x^2+(y-p)^2=9\)・・・②
①より
\(x^2=8y\)・・・③
③を②に代入して
\(8y+(y-p)^2=9\)
整理すると
\(y^2-2(p-4)y+p^2-9=0\)・・・④
\(\displaystyle\frac{D}{4}=(p-4)^2-(p^2-9)\)
\(=-8p+25\)
(i)\(D<0\) のとき
\(p>\displaystyle\frac{25}{8}\) のとき、④の解は虚数解。よって共有点はない。
(ii)\(D=0\) のとき
\(p=\displaystyle\frac{25}{8}\) のとき、④は1つ実数解(重解)をもつ。その解は
\(y=p-4=\displaystyle\frac{25}{8}-4=-\displaystyle\frac{7}{8}<0\)
よって③より\(x\)は虚数となるので、共有点はない。
(iii)\(D>0\) のとき
\(p<\displaystyle\frac{25}{8}\) である。
④の左辺で \(y=0\) とすると \(p^2-9\)。この値の正負と④の左辺を2次関数とみたときの軸\(p-4\ (<0)\)に着目する。④の解の正負について
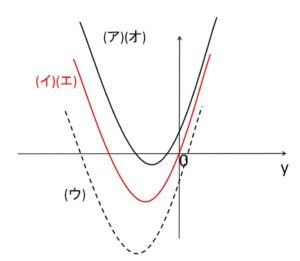
(ア)\(3<p<\displaystyle\frac{25}{8}\) のとき
異なる2つの負の実数解をもつので、対応する実数\(x\)はない。よって共有点はない。
(図は(i)(ii)と同じ)
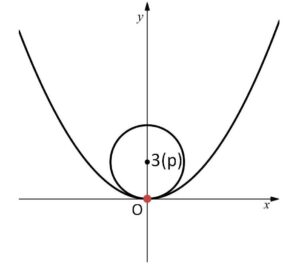
(イ)\(p=3\) のとき
\(0\)と負の解をもつ。よって対応する実数\(x\)は1つなので、共有点は1つ。
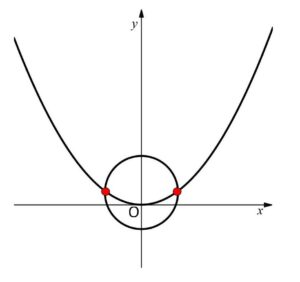
(ウ)\(-3<p<3\) のとき
正と負の解を1つずつもつ。よって対応する実数\(x\)は2つなので、共有点は2つ。
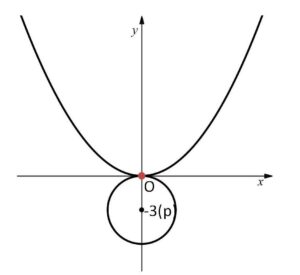
(エ)\(p=-3\) のとき
\(0\)と負の解をもつ。よって対応する実数\(x\)は1つなので、共有点は1つ。
(オ)\(p<-3\) のとき
異なる2つの負の実数解をもつので、対応する実数\(x\)はない。よって共有点はない。
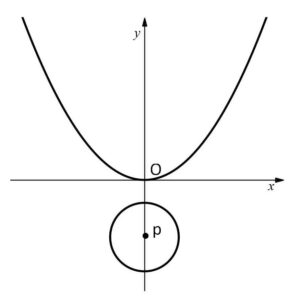
以上をまとめると
\(p>3\) のとき 共有点はない
\(p=3\) のとき 1つ
\(-3<p<3\) のとき 2つ
\(p=-3\) のとき 1つ
\(p<-3\) のとき 共有点はない
(2)
円の上端と下端における接線は\(x\)軸に平行。よって(1)の結果より2曲線が接するのは
\(p=3,-3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡の基礎 back→円上の動点と円上にない定点の距離