まずは中学までに習った知識の復習です。
高校範囲の内容も少し含めてまとめたいと思います。
・三角形の合同
ある2つの平面図形があるとき、一方を「平行移動・回転移動・対称移動」することでもう一方に重ね合わせることができるとき、その2つの図形は合同であるといいます。簡単にいうと大きさも形も一緒の図形ということです。
三角形の合同条件は次のように習います。
(1)3辺が等しい
(2)2辺とその間の角が等しい
(3)1辺とその両端の角が等しい
これらは座標平面や余弦定理・正弦定理などを利用することで示すことが可能です。
実は(3)については、三角形の内角の和が\(180°\)であることから、2つの角が等しいことが分かればよく、両端の角である必要性はありません。しかし、(2)の角については間の角でとる必要があります。
また直角三角形の合同条件は次のように習います。
(1)斜辺と1つの鋭角が等しい
(2)斜辺と他の1辺が等しい
一般の三角形の合同では条件がそれぞれ3つ(3辺、2辺と1角、1辺と2角)ですが、直角三角形では条件が2つ(斜辺と1角、斜辺と1辺)に減っています。また個数も1つ減っています。これらは、直角三角形であることから「1角が直角と分かっている、2辺が分かると三平方の定理よりもう1辺が分かる」ことが理由です。
なお、直角三角形であっても一般の三角形の合同条件を使ってももちろん構いません。
・二等辺三角形の性質
2辺が等しい三角形を二等辺三角形とよびます。
二等辺三角形には次の性質があります。
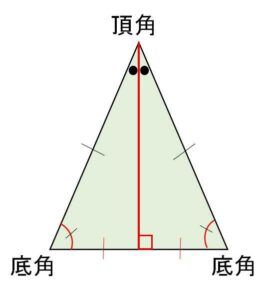
(1)底角が等しい
(2)頂角の頂点から中線を下ろすと、頂角と底辺をそれぞれ二等分する。また中線は垂線となる。
2つに分けられてた三角形が合同であることから分かります。
また、3辺が等しい三角形は正三角形とよばれます。正三角形は二等辺三角形の特殊例になり、上記性質が成り立ち、(1)より3つの内角がすべて\(60°\)で等しくなります。
また(1)については逆に
(1)’2つの内角が等しければ、二等辺三角形
も成立します。補助線として、残りの角の頂点から角の二等分線を引くか垂線を下ろすかすれば証明できます。
・三平方の定理
(三平方の定理)
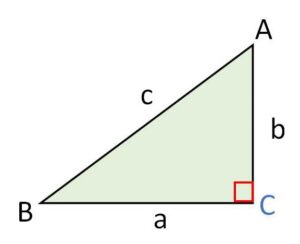
\(\angle C=90°\) である直角三角形\(△ABC\)において、図のように3辺の長さを\(a,b,c\)とすると
\(a^2+b^2=c^2\)
が成り立つ。
(三平方の定理の逆)
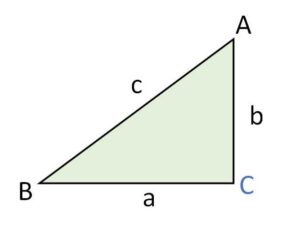
三角形\(△ABC\)において、図のように3辺の長さを\(a,b,c\)とすると
\(a^2+b^2=c^2\)
が成り立てば、\(△ABC\) は \(\angle C=90°\) の直角三角形である。
(解説)
直角三角形であることが判明している場合に、2乗和の等式が成り立つのが三平方の定理です。
一方、直角三角形であることが判明していなくても2乗和の等式が成り立てば \(\angle C=90°\) の直角三角形であることが分かるのが三平方の定理の逆です。
一般にある命題が真であるときにその逆も真であるとは限りませんが、これは逆も真になっているケースです。三平方の定理の証明は今回は省略することにして、その逆について証明したいと思います。
(逆の証明)
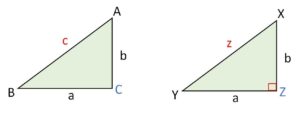
2辺が\(a,b\)で、これらにはさまれる角が直角である\(△XYZ\)を用意する。
\(△XYZ\)の斜辺を\(z\)とすれば、三平方の定理より
\(a^2+b^2=z^2\)・・・①
条件より
\(a^2+b^2=c^2\)・・・②
①②より
\(z=c\)
よって3辺が等しいことから
\(△ABC≡△XYZ\)
したがって
\(\angle C=\angle Z=90°\)
この方法はとりあえず\(c\)とは異なるとした斜辺\(z\)を設定して、\(c,z\)が一致することを示していて、同一法(一致法)とよばれます。同一法は図形の証明でよく利用されます。
・三角形の相似
ある2つの図形があり、一方の図形を形をそのままに拡大縮小した図形がもう一方の図形になるとき、これらの図形は相似であるといいます。
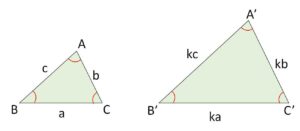
三角形の相似について考えます。3辺が\(a,b,c\)である\(△ABC\)があり、これを\(k\)倍拡大縮小した三角形を\(△A’B’C’\)すると、この三角形の3辺は\(ka,kb,kc\)となり、余弦定理より3つの内角がそれぞれ等しいことが分かります。逆に3内角がそれぞれ等しいとき、正弦定理により3組の辺の比が等しいことが分かります。
すると次の三角形の相似条件が納得できます。
(1)3組の辺の比が等しい
(2)2組の辺の比とその間の角が等しい
(3)2組の角が等しい
(3)で2つの角で済んでいる理由は、三角形の内角の和が\(180°\)であることから、もう1つの角が自動的に決まるからです。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→平行と線分比