チェバの定理について見ていきます。
・チェバの定理
線分比の積について次のことが成り立ちます。
\(△ABC\)の3頂点\(A,B,C\)と、三角形の辺上またはその延長上にない点\(O\)とを結んで3直線をひく。3直線\(AO,BO,CO\)が対辺\(BC,CA,AB\)またはその延長と交わるとき、交点をそれぞれ\(P,Q,R\)とすると
\(\displaystyle\frac{BP}{PC}⋅\displaystyle\frac{CQ}{QA}⋅\displaystyle\frac{AR}{RB}=1\)
(解説)
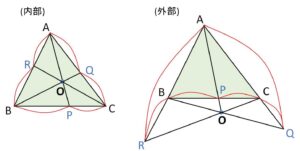
\(O\)の取り方は三角形の内部だけでなく外部でもよいです。図は異なりますが結果も証明方法も同じです。ただし三角形をつくる直線上に\(O\)をとってしまうと、分数の分母が\(0\)になってしまう箇所がでてくるのでこれは除かれます。結果の分数式はやや複雑ですが、図を参照して「頂点→中継(分点)→頂点→中継(分点)→」の繰り返しであることに着目すると覚えやすいと思います。スタートの頂点は上の式では\(B\)になっていますが、積の順序は交換可能なのでどの頂点からスタートしても構いません。
証明は2つ紹介します。
(証明1)面積比を利用
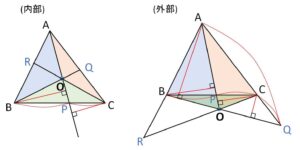
面積比を線分比で表して積(場合によっては逆数の積)をとればよい。
\(\displaystyle\frac{△OAB}{△OAC}=\displaystyle\frac{BP}{PC}\)・・・①
\(\displaystyle\frac{△OBC}{△OAB}=\displaystyle\frac{CQ}{QA}\)・・・②
\(\displaystyle\frac{△OAC}{△OBC}=\displaystyle\frac{AR}{RB}\)・・・③
①②③の辺々を掛けて
\(1=\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}\)
(証明2)平行線を利用
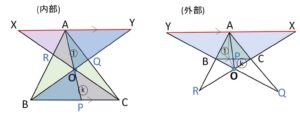
\(A\)を通り\(BC\)に平行な直線(補助線)をひき、\(CO,BO\)との交点を\(X,Y\)とおく。
\(AO:OP=1:k\) とすると、平行線の線分比を考えて
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}\)
\(=\displaystyle\frac{kAY}{kAX}\cdot\displaystyle\frac{BC}{AY}\cdot\displaystyle\frac{AX}{BC}\)
\(=1\)
・チェバの定理に似た定理(線分比の和の定理)
線分比の和の定理もせっかくなのでここで紹介します。
\(△ABC\)の内部に1点\(O\)をとり、直線\(AO,BO,CO\)がそれぞれ辺\(BC,CA,AB\)と交わる点を順に\(P,Q,R\)とすると
\(\displaystyle\frac{OP}{AP}+\displaystyle\frac{OQ}{BQ}+\displaystyle\frac{OR}{CR}=1\)
(証明)
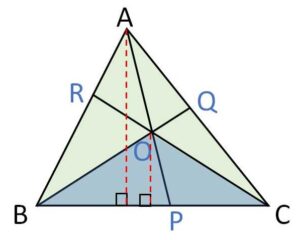
(チェバの定理と同様に面積比で考えます)
底辺の等しい三角形の面積比は高さの比だから、平行線の線分比も考慮して
\(\displaystyle\frac{△OBC}{△ABC}=\displaystyle\frac{OP}{AP}\)・・・①
同様に、底辺\(CA,AB\)について
\(\displaystyle\frac{△OCA}{△ABC}=\displaystyle\frac{OQ}{BQ}\)・・・②
\(\displaystyle\frac{△OAB}{△ABC}=\displaystyle\frac{OR}{CR}\)・・・③
①+②+③より
\(\displaystyle\frac{△OBC+△OCA+△OAB}{△ABC}=\displaystyle\frac{OP}{AP}+\displaystyle\frac{OQ}{BQ}+\displaystyle\frac{OR}{CR}\)
よって
\(\displaystyle\frac{△ABC}{△ABC}=\displaystyle\frac{OP}{AP}+\displaystyle\frac{OQ}{BQ}+\displaystyle\frac{OR}{CR}\)
\(1=\displaystyle\frac{OP}{AP}+\displaystyle\frac{OQ}{BQ}+\displaystyle\frac{OR}{CR}\)
(例題)
\(△ABC\)の辺\(AB,AC\)に交わるような\(BC\)に平行な直線をとり、これらの交点を\(D,E\)とする。\(BE,CD\)の交点を\(O\)とし、直線\(AO\)と\(BC\)の交点を\(F\)とする。\(F\)は\(BC\)の中点であることを示せ。
(解答)
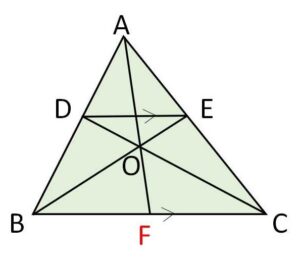
\(\displaystyle\frac{BF}{FC}\cdot\displaystyle\frac{CE}{EA}\cdot\displaystyle\frac{AD}{DB}=1\)・・・①
また\(DE//BC\)より
\(\displaystyle\frac{AD}{DB}=\displaystyle\frac{EA}{CE}\)・・・②
②より
\(\displaystyle\frac{CE}{EA}\cdot\displaystyle\frac{AD}{DB}=1\) だから①より
\(\displaystyle\frac{BF}{FC}=1\)
したがって
\(BF=FC\) だから、\(F\)は中点である。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→メネラウスの定理 back→オイラー線